動円の半径を１とすると，ｎ尖点エピサイクロイドとｎ尖点ハイポサイクロイドの間の鉢形曲線については

　　Ｌ＝（８（ｎ＋１）＋８（ｎ−１））／ｎ＝１６

　　Ｓ＝（（ｎ＋１）（ｎ＋２）−（ｎ−１）（ｎ−２））／ｎπ＝６π

が成り立ちます．

　（その１２）ではｎ＝１，ｎ＝２についてもこれらの式が成り立つことをみてきました．ｎ＝２では直径を固定点の軌跡が固定円の直径を往復すると考えて

　　Ｌ＝（２４＋８）／２＝１６，Ｓ＝（１２）／２π＝６π

としたほうがいいようです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

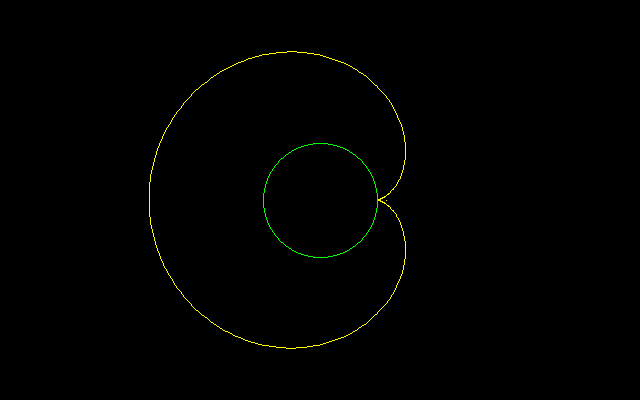
［１］カージオイド

　内側の曲線は動くことができず，弧長Ｌは０，面積Ｓも０になるので，外側のカージオイド曲線ではＬ＝１６，Ｓ＝６πとなります．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

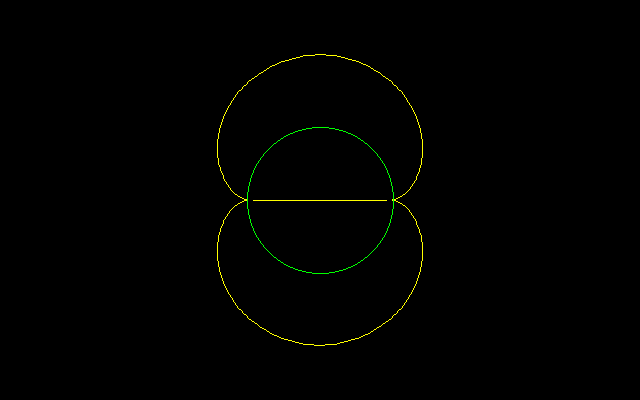
［２］ネフロイド

　内側の曲線は円の直径になります．したがって，弧長Ｌは８，面積Ｓは０になる．外側のネフロイド曲線では

　　面積：（ｎ＋１）（ｎ＋２）π＝１２π

　　弧長：８（ｎ＋１）＝２４

また，半円

　　面積：０

　　弧長（直径）：４

　　Ｌ＝（２４＋８）／２＝１６，Ｓ＝（１２）／２π＝６π

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝