このシリーズでは，はなまるを

［１］半径１の円の円周上でｎ個の円が接する

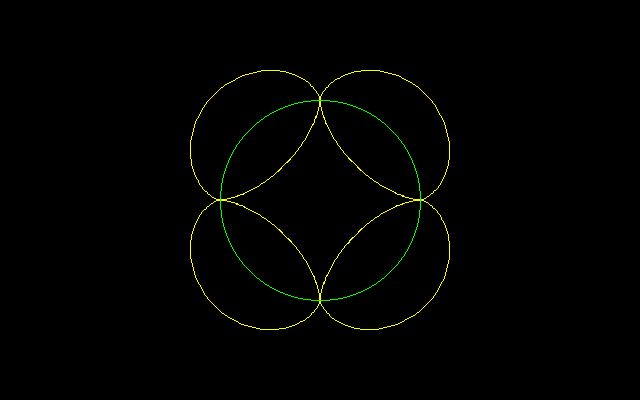
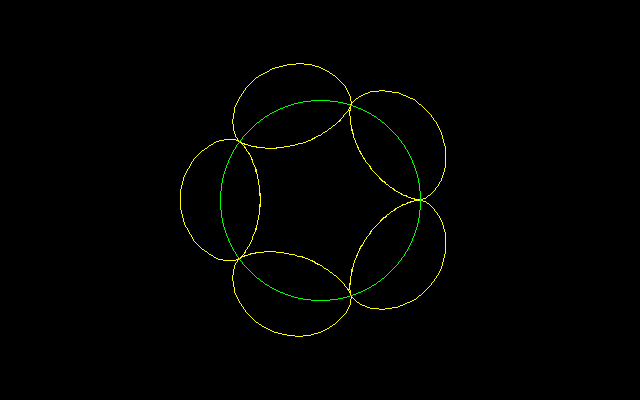
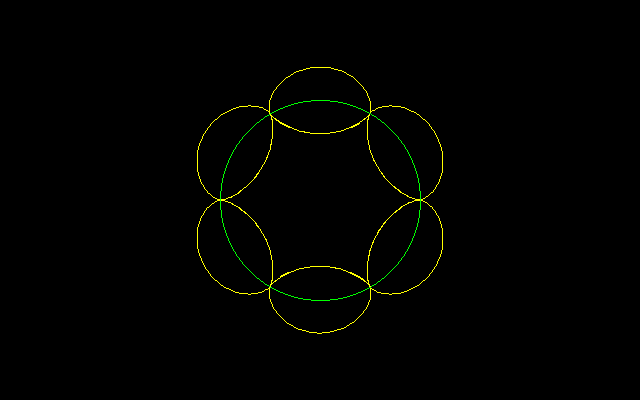
［２］半径１の円の円周上でｎ個の円が直交する

ように描いてきたが，今回は，

［１］半径１の円の円周上でｎ尖点ハイポサイクロイドが円に接する（直交する）

［２］半径１の円の円周上でｎ尖点エピサイクロイドが円に接する（直交する）

ように描いてみる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［１］カージオイドではＬ＝１６，Ｓ＝６π

　一般に，ｎ尖点ハイポサイクロイドでは

　　面積：（ｎ−１）（ｎ−２）π

　　弧長：８（ｎ−１）

ｎ尖点ハイポサイクロイドでは

　　面積：（ｎ＋１）（ｎ＋２）π

　　弧長：８（ｎ＋１）

［２］デルトイド

　　ｘ＝２ｃｏｓθ＋ｃｏｓ２θ

　　ｙ＝−２ｓｉｎθ＋ｓｉｎ２θ

と３尖点エピサイクロイド

　　ｘ＝４ｃｏｓθ−ｃｏｓ４θ

　　ｙ＝４ｓｉｎθ−ｓｉｎ４θ

で囲まれる１区間でもＬ＝１６，Ｓ＝６π．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝