（その１）（その２）で述べたことは有名な幾何の問題であるが，以上の関係が追跡曲線の問題の解を得るのに重要であるとは気づきにくいだろう．

　正方形の４つの頂点の１匹ずつ犬がいる．それぞれ，同じ速さで隣の犬を追いかけたとする．それぞれの犬はいつも前方にいる犬に向かって同じスピードで進む．４匹の犬を結ぶ図形は回転しながら次第に小さくなる正方形になり，元の正方形の中心で出会うことになる．

［Ｑ］このとき犬のたどる軌跡は？

［Ａ］等角らせん

［Ｑ］正方形の１辺の長さは３０ｍ，それぞれの犬は１ｍ／ｓの速度で動くとする．犬達が正方形の中心で出会うのにどれくらいの時間がかかるか？

［Ａ］等角らせんの伸開線と縮閉線は，もとの等角らせんと合同な等角らせんになる．犬の進む経路と正方形の１辺の長さは等しいからら，３０秒．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ｎ匹のイヌが正ｎ角形の頂点に１匹ずついたとして，それぞれ同じ速さで隣りのイヌを追いかけるとする．この場合も，イヌのたどる軌跡は等角らせんになる．

［１］回転する正三角形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

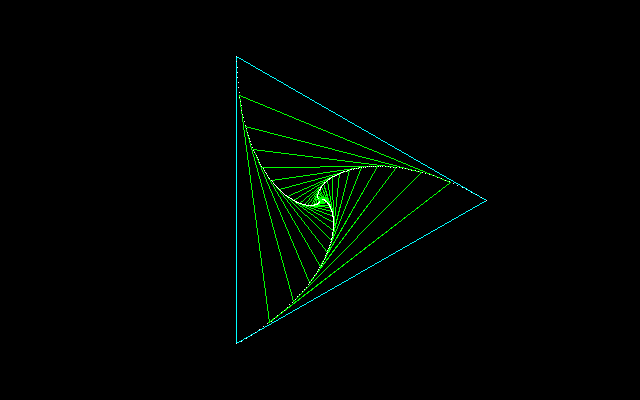
［２］回転する正方形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［３］回転する正五角形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［４］回転する正六角形の追跡問題

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝