直前の叙述は立方体切頂面にある８枚の正三角形についてでした。

最初の角度４５度は正三角形の面の重心を、正方形面からの投影図で方位を表しています。

次の角度３５．２６度は三角形面が天地軸となす角度を示しています。

同じ関係を、ねじれ立方体の正方形面と辺を共有している三角形について調べたものがあの表だと思われます。

左の列の角度については投影図を使って対応が確認できました。

しかし右の列の角度、つまり三角形面と天地軸とのなす角度は一般的な投影図では確認できません。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

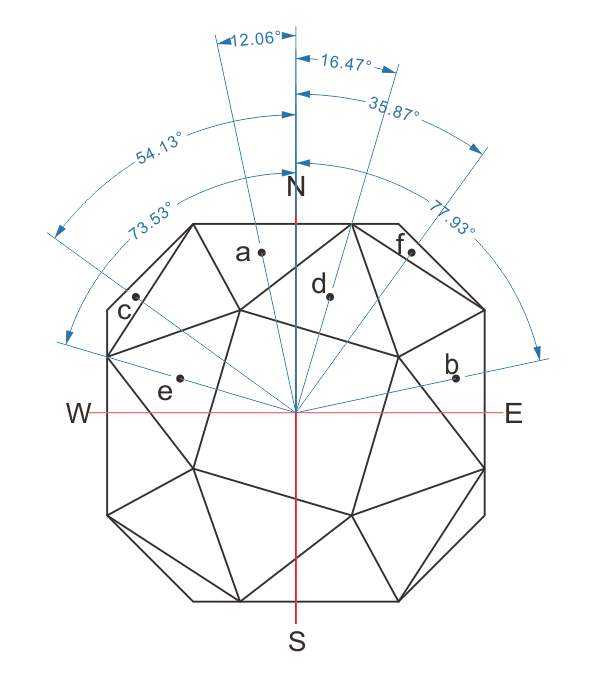
6枚の正方形の頂点は

[(t,1,1/t),(t,-1/t,1),(t,-1,-1/t),(t,1/t,-1)]

[(-t,1/t,1),(-t,-1,1/t),(-t,-1/t,-1),(-t,1,-1/t)]

[(1/t,t,1),(1,t,-1/t),(-1/t,t,-1),(-1,t,1/t)]

[(1,-t,1/t),(1/t,-t,-1),(-1,-t,-1/t),(-1/t,-t,1)]

[(1,1/t,t),(-1/t,1,t),(-1,t,-1/t,t),(1/t,-1,t)]

[(1/t,1,-t),(-1,1/t,-t),(-1/t,-1,-t),(1,-1/t,-t)]

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

座標データの入力ミスがあり、表の数値となかなか一致しなかったが、やっと合致。

表の左右の列の数値も同じ面に対応していることも確認された。

左の列は面の中心と中心(0,0,0)を結ぶベクトル(x,y,z)が投影図上ｘ軸、ｙ軸、ｚ軸となす角度

右の列は面の法線ベクトル(x,y,z)がｘ軸、ｙ軸、ｚ軸となす角度で与えられることが確かめられた。

後者はcosθ=x/(x^2+y^2+z^2)^1/2,cosθ=y/(x^2+y^2+z^2)^1/2,cosθ=z/(x^2+y^2+z^2)^1/2で計算できるが、

前者はcosθ=x/(x^2+y^2)^1/2,y/(y^2+z^2)^1/2,z/(z^2+x^2)^1/2となることに注意

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝