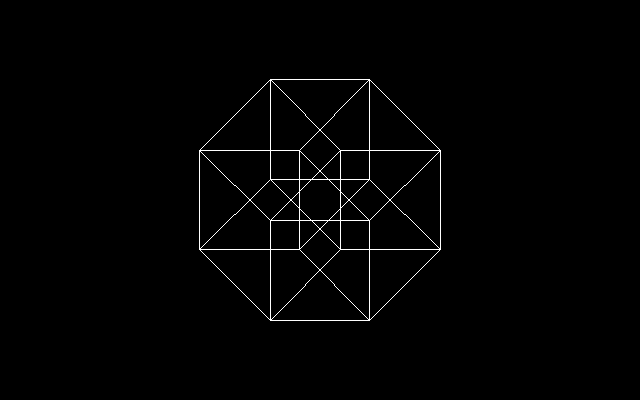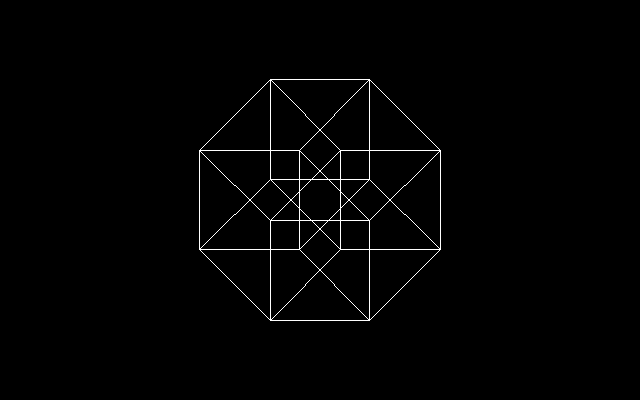本シリーズをまとめておきたい．このシリーズでは，ｎ次元立方体・正軸体・正単体を２次元平面上に複数の頂点がなるべく重ならないように座標軸をとって，実際に描く方法について考察した．

　４次元立方体・正軸体・正単体の場合を実際に描くことをを試みた．その表示法はワイヤーフレームモデルであって，ワイヤーフレームモデルは図形を網目として素通しで見るものであるから，ややリアリティーに欠けるものの，複雑な手順を必要としない最も簡単な表示法である．

　そのため，以下の図はそれぞれ正８角形，正８角形，正五角形に適当に対角線を引いたように見えるかもしれないがそうではない！

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［１］４次元立方体の２次元投影図

　白銀比は正八角形と密接な関係にある．正八角形に３／８角形を書き入れると正八角形できるが，この手順を繰り返すと，正八角形と星形８／３角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．ところで，この図形は４次元立方体の２次元投影図でもある．

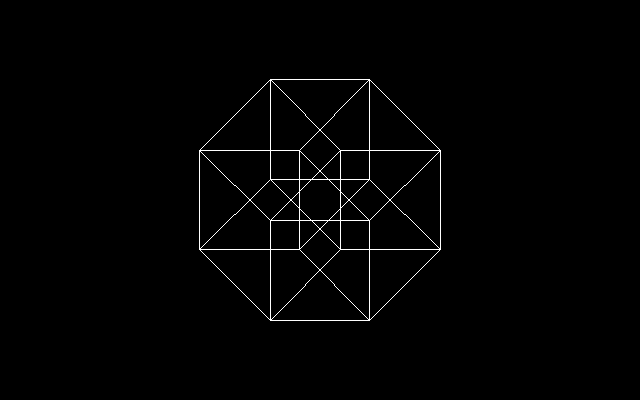
　ｎ次元立方体では，ｎが２のベキ（ｎ＝２，４，８，１６，・・・）のとき，中心部に穴が開く．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［２］４次元正軸体の２次元投影図

　ｎ次元正軸体では，ｎのパリティ−に関わらず，中心部に穴が開く．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［３］４次元正単体の２次元投影図

　黄金比は正五角形と密接な関係にある．正五角形に対角線を書き入れると星形五角形できるが，この手順を繰り返すと，正五角形と星形五角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．正五角形に対角線を描き入れると星形五角形（ソロモンの星）ができるが，正五角形と星形五角形の入れ子はペンタグラムと呼ばれる．この図形が４次元正単体の２次元投影図であることを知っている人は少ないだろう．

　ｎ次元正単体の場合は，ｎが偶数のとき中心部に穴が開く．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝