■ペンタゴンとペンタグラム(その13)
【1】3次元立方体の投影図
3次元立方体を(1,1,1)方向に投影すると,2次元投影図は正六角形になる.
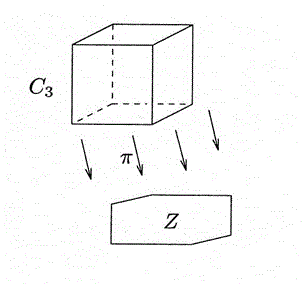
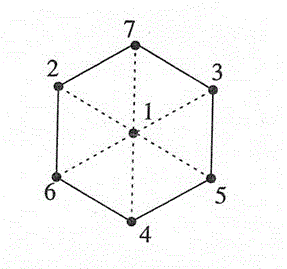
最近の若い人の中には,この図を見て「三角形が6つ合わさった形」と答える人がいるとのことである.この答えは間違いではないが,立体図形に見えないのなら少々問題があるだろう.
以下のロゴは,東北大学金属材料研究所のものであるが,川添良幸先生から聞いた話では「この六角形が立方体に見えぬ者はこの門をくぐるなかれ」といったことを意味しているそうである.


===================================
【2】4次元立方体の投影図
以下にイメージミッション社のロゴを掲げるが,この図は4次元立方体の3次元投影図である.

===================================
【3】n次元立方体の投影図
正方形(2次元立方体)を平面に投影すると正方形,3次元立方体を投影すると正六角形,4次元立方体を投影すると正八角形になる.
3次元立方体の8つの頂点を第4の方向に1単位だけ平行移動することにより,4次元立方体の3次元投影図を描くことができるからである.一般に,n次元立方体の投影図は正2n角形となることがおわかり頂けるであろう.
次に,投影図形の中央に穴が開くかどうかに注目してみよう.正方形(2次元立方体)を平面に投影した場合は穴が開く.3次元立方体の平面投影図は三角形が6つ合わさった形になり,穴は開かない.4次元立方体の平面投影図には穴が開く.
これについては,nが2のベキ(n=2,4,8,16,・・・)のとき,中止部に穴が開くのが見てとれるだろう.
===================================







