■最も有名な超越数(その23)
0<(e^π−π^e)<1
を示したい.
===================================
【1】わかっていること
[1]x^y−y^x=1の整数解は(x,y)=(3,2)だけである(3^2−2^3=1).すなわち,8と9だけが唯一連続するベキ乗数である.
[2]x^y−y^x=0 (0<x<y)
2≦x<e<y≦4で,(x,y)がともに整数となるのは(x,y)=(2,4)のみである(4^2−2^4=0).
[3](x,y)=(e,e),したがって,e^e=15.1542・・・の周囲にx^y−y^x=0となる解が集積する.
[4]x=2〜3,y=3〜4にはy^x−x^y=1となる解が分布する.
===================================
【2】Mathematicaによるグラフ表示
e^π=23.14069・・・≒π+20
π^e=22.45915・・・
となるが,π^eについては,昔なら数表を使うか,計算尺(LL尺付き)を使うことになるが,Mathematicaにx^y-y^x=0をyについて解くための適切な特殊関数の機能があった.
[1]x^y−y^xの等高線表示
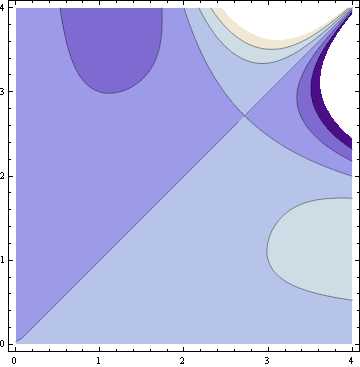
[a]x^y−y^x=0
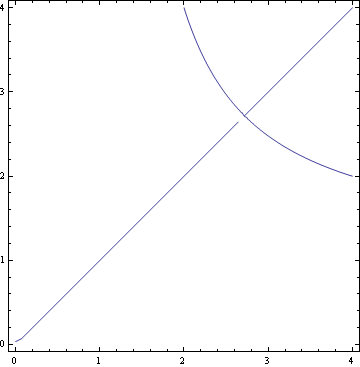
[b]x^y−y^x=1

===================================
【3】Mathematicaによる解析
x^y-y^x=0のyの解析解は得られるが,x^y-y^x==1をyに関して解くことは出来ないようだ.よって,Solve,NSolveで解を求めることは出来なかった. (阪本ひろむ)
f(y)=e^y−y^e−1の数値解は
0,
1.87422,
3.21736・・・y=πは結構ぎりぎりの線なのである.
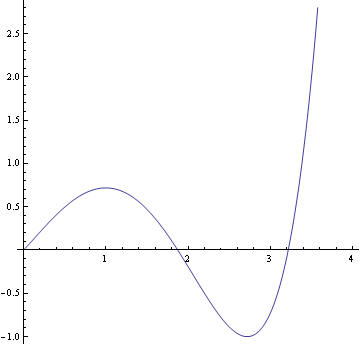
===================================






