[Q]正ｎ角形→正方形でもできるのですか？

[A]はい

[Q]最少ピースの数に規則性はありますか？

[A]ないと思います

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Frederickson "Dissections"で探してみたところ、

P118に５片で正六角形→正方形

P120に６片で正五角形→正方形

P276に５片で正五角形→近似正方形

の図が載っていました。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正六角形の１辺の長さを1とする

面積は1/2・3√3=a^2

菱形と正三角形にみえるが、いずれも不等辺である。

平行移動だけで正方形ができる。回転は不要である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

y=mxとy=1/2・√3の交点を求める。

x=1/2m・√3,y=1/2・√3

x^2+y^2=a^2

3/4m^2+3/4=a^2→ｍが求まる→xが求まる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

(3/2,-√3/2)を通る傾き-1/mの直線は

YY+√3/2=-1/m(XX-3/2)

x軸との交点は

XX=3/2-m√3/2

長さの２乗は(XX-3/2)^2+3/4=3m^2/4+3/4＝b

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

(x0,0)からy=mxまでの距離の２乗は

(mx0)^2/(m^2+1)=c

√b+√c=aよりｘ0を求める

y=mxとy=-1/m(x-x0)の交点を求める

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

中川宏さんがこの解体再編を図示してくれたので、掲載する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
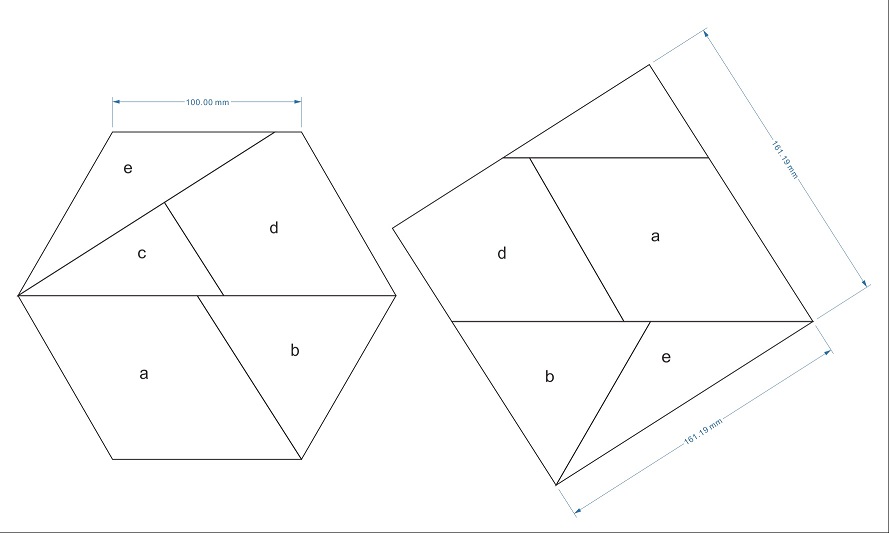