■正五角形と正方形のカンタベリー・パズル(その7)
デュドニーは正三角形を4片に分解してそれを組み替えなおして正方形をつくるパズルを創作した。
彼は正五角形を組み替えなおして正方形をつくるパズルも創作している。
ここでの問題は最小個数の部品の分割することである。
====================================
デュドニー自身の答えは6片というものであった。
====================================
デュドニーは5片の断片を使った答えを読者から受け取ったという。
しかし、その答えは近似的な正方形にしかならなかったが、答えに極めて近く目では間違いを見抜くことができなかった。
正五角形の対角線の半分に正五角形の辺の半分を足せばφ/2+1/2=φ^2/2となるが
同面積の正方形の辺長=1/2・(√5φ)^3/4〜13/10に極めて近い。
Frederickson "Dissections"
P276に5片で正五角形→近似正方形
の図が載っている。
====================================
この近似作図法は対角線の二等分点1か所と辺の二等分点3か所をつなぐものであるが、どれくらいの誤差となるのだろうか。
正三角形を正方形に変身させるカンタベリーパズルでも、辺の四等分点で近似するものがあるがそれと同程度の誤差で済むだろうか?
中川宏さんが近似的な解体再編法の図を送ってくれたので、掲載する。
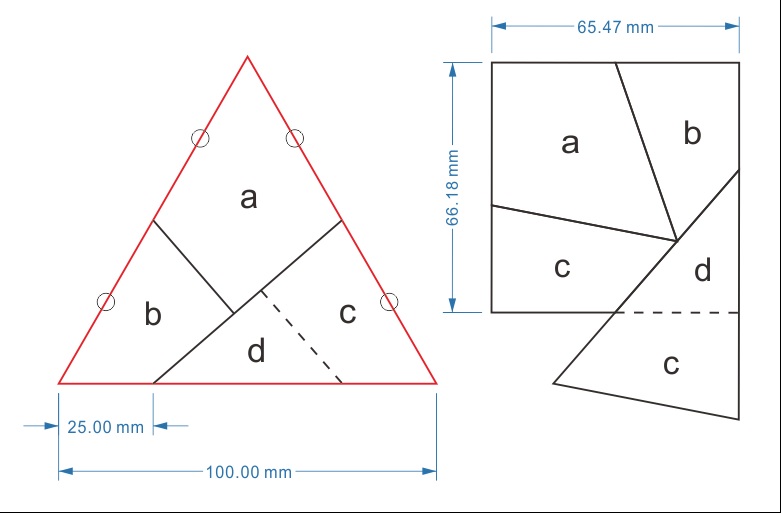
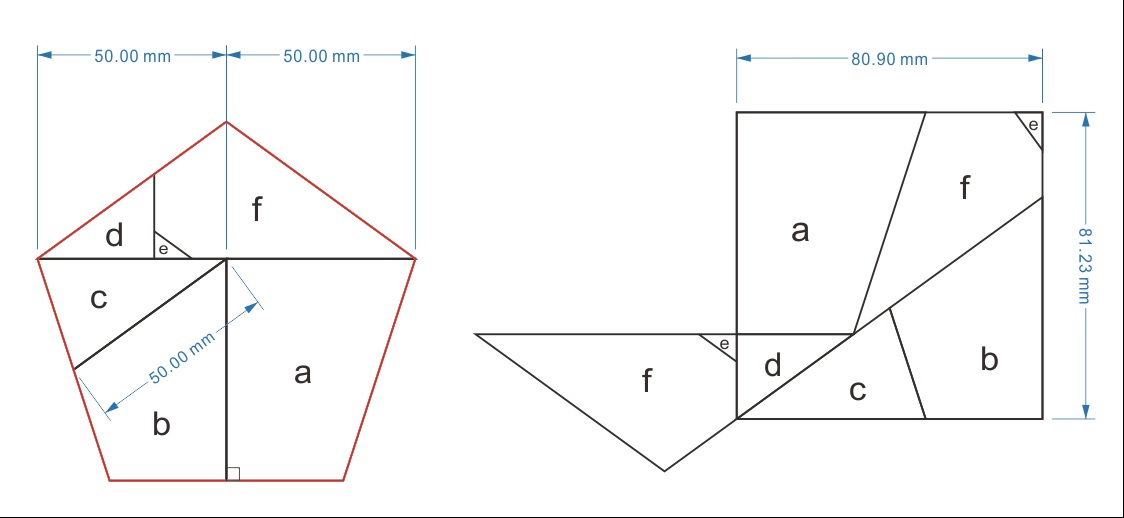
====================================




