メルカトール図法の歪曲は極の近くで大きくなり、極自体を表示することはできなくなる。

北緯７２度の緯線上のグリーンランドの面積は

実際の面積よりも1/(cos72)^2=10.47倍も大きくなります。

その結果、南アメリカ大陸と同じくらいの面積を持つように見えるのです。

cos72=1/(2τ)

1/(cos72)^2=4τ^2＝4:2.618=10.472

面積を保つ投影法を使えばこうはなりません。

面積を保つ等積投影法とは数学的にはどういうことだろうか？

変換のヤコビアンが１に等しく、いかなる領域の面積も変わらない（J=1）ことなのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

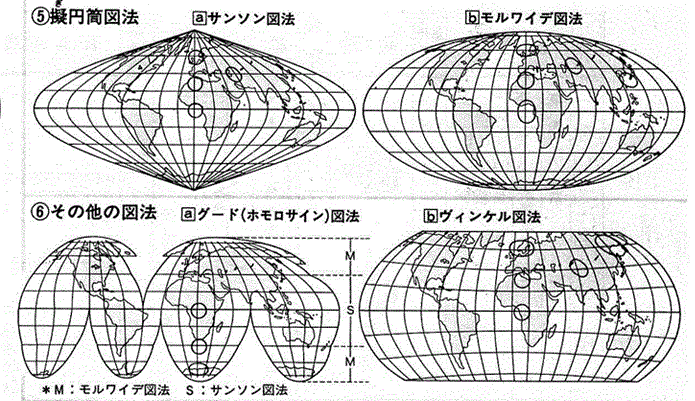
　高校の地理の問題である．地図投影法に

［１］サンソン図法・・・経線は正弦曲線，高緯度部分でひずみが大きい

［２］モルワイデ図法・・・経線は楕円，高緯度部分でひずみが大きい

［３］グード図法・・・サンソン図法の低緯度部分，モルワイデ図法の高緯度部分の長所を活かし，緯度４０°４４′で接合したもの

とある（が，緯度４０°４４′で緯線の長さが等しいようにはどうしてもみえない．）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ヤコビアン

　一般に，関数の１階偏微分行列式

　　Ｊ＝｜ｆx ｆy ｜

　　　　｜ｇx ｇy ｜

はヤコビアンと呼ばれるものであり，３変数の場合のヤコビアンは，

　　｜ｆx ｆy ｆz ｜

　　Ｊ＝｜ｇx ｇy ｇz ｜

　　　　｜ｈx ｈy ｈz ｜

と書くことができます．

　ヤコビアンはヤコビの名をとどめる行列式ですが，ヤコビが先鞭をつけた関数行列式はヘッセなどに引き継がれ，解析幾何学の面でたびたび利用され発展しました．

　ヘッセにもヘシアンという彼の名をとどめる２階偏微分行列式があり，２変数の場合は，

　　Ｈ＝｜ｆxx ｆxy ｜

　　　　｜ｆyx ｆyy ｜

３変数の場合は，

　　 ｜ｆxx ｆxy ｆxz ｜

　　Ｈ＝｜ｆyx ｆyy ｆyz ｜

　　　　｜ｆzx ｆzy ｆzz ｜

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ケーラーのヤコビアン予想

これらの変換にとって望ましい性質の一つは「逆変換」が存在するということである。

しかし、大域的に可逆、すなわと全平面で逆関数が存在するかどうかはわからない。

大域的に可逆でない例が知られているが、１９３９年ケーラーは変換のすべての成分が多項式ならば、変換は大域的に可逆で、逆関数も多項式になると予想した。

この問題はケーラーのヤコビアン予想と呼ばれ、まだ解決されていない（2次元では成り立つが高次元では成り立たないと広く信じられている）。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝