■格子点と追跡曲線(その12)
正多角形の頂点を格子点に置くことは可能であろうか?
頂点を中心としてそれぞれの辺を時計回りに90°回転させると、その軌跡は追跡曲線によく似た円弧になる。
円弧を連結させた曲線であるから、黄金長方形のなかの正方形に四半円弧を連結させた近似黄金らせんに類似したものになると思われる。
正五角形の場合
(1,0)→(0,1)に移る90°回転を考えると,もう一つの頂点は
[cos90,-sin90][-cos108]+[cos108]=[sin108+cos108]
[sin90, cos90][-sin108] [sin108] [-cos108+sin108]
に移るから、1辺の長さの2乗は
(sin108+cos108)^2+(sin108-cos108-1)^2
=2+2cos108-2sin108+1
=4(cos54)^2-4sin54cos54+1<1
-90度について長さがX={4(cos54)^2-4sin54cos54+1}^1/2倍になる対数らせんで近似できることになる。
r=exp(aθ)
r=exp(a(θ+π/2))=(exp(aπ/2))exp(mθ)
(exp(aπ/2))=Xでaを定めればよいことになる
===================================
正五角形の頂点がすべて格子点だったと仮定すると場合、元に正五角形の内側に頂点が格子点上にある正五角形ができる。
この手続きを繰り返すと頂点が格子点上にあるいくらでも小さな正五角形ができてしまうが、これは矛盾である。
正方形以外のどのような正多角形(正三角形でも正六角形でも)そのようにすることは不可能なのである。
===================================
[1]回転する正三角形の追跡問題
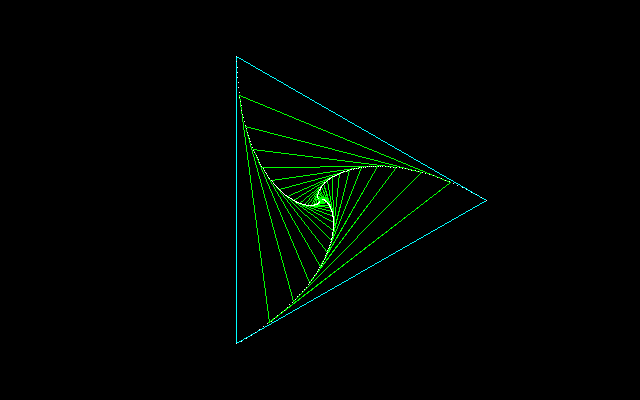
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[2]回転する正方形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[3]回転する正五角形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[4]回転する正六角形の追跡問題

===================================






