仭嶰偮愜傝偺庤巻乮偦偺俀乯
丂暯峴巐曈宍偺捀揰俙丆俛丆俠丆俢傪偦傟偧傟曈俛俠丆俠俢丆俢俙丆俙俛偺拞揰偲寢傫偱丆拞墰偵彫偝偄暯峴巐曈宍傪嶌傞丏偙偺彫偝偄暯峴巐曈宍偺柺愊偼丆傕偲偺暯峴巐曈宍偺柺愊偺侾乛俆偵摍偟偄丏師偵丆暯峴巐曈宍偺捀揰俙丆俛丆俠丆俢傪偦傟偧傟曈俠俢丆俢俙丆俙俛丆俛俠偺拞揰偲寢傫偱傕拞墰偵彫偝偄暯峴巐曈宍偑摼傜傟傞丏偙偺彫偝偄暯峴巐曈宍偑廳側偭偨晹暘偼揰懳徧側俉妏宍偱丆偦偺柺愊偼傕偲偺暯峴巐曈宍偺柺愊偺侾乛俇偵摍偟偄丏
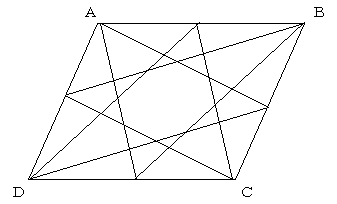
丂偙偺偲偒丆廳側偭偰偄傞彫偝偄暯峴巐曈宍偼屳偄偺曈傪俁摍暘偡傞偺偱偼側偔丆曈傪暘妱偡傞斾偼係丗俆丗俁偵側偭偰偄傞丏丏
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
乮嘥乯暯峴巐曈宍偺捀揰偲岦偐偄偺曈偺拞揰傪傓偡傇慄暘偼丆係捀揰偲係拞揰偺偄偢傟偐傪椉抂偲偡傞偡傋偰偺慄暘偵傛偭偰丆俇丗係丗俆丗俁丗俀丗侾侽偺斾偵暘妱偝傟傞丏
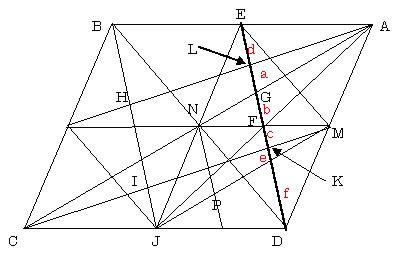
乮徹乯暯峴巐曈宍偺拞慄掕棟偵傛傝丆慄暘DE偵偍偄偰丆
丂丂2(d+a)=b+c+e+f丂丒丒丒嘆
丂 a+d=2b=f=e+c丂丒丒丒嘇
嶰妏宍俙俴俢偵偍偄偰丆AL偲MK偼暯峴側偺偱丆
丂丂a+b+c=e+f丂丒丒丒嘊
嶰妏宍俙俛俫偵偍偄偰丆BH偲EL偼暯峴側偺偱丆
丂丂2d=BH=e+f=a+b+c
丂丂4d=a+b+c+e+f 丒丒丒嘋
嘆偲嘋偐傜丆3a=2d
丂嶰妏宍俙俤俧偲嶰妏宍俵俶俹偼崌摨側偺偱丆d:a亖c:e
傛偭偰丆f=10偲偍偔偲丆a+d=10丆d=6丆a=4丆b=(a+d)/2=5丆c+e=5丆c=3丆e=2
偲側傝丆慄暘俤俢偼丆俇丗係丗俆丗俁丗俀丗侾侽偵暘妱偝傟偰偄傞偙偲偑傢偐偭偨丏
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
乮嘦乯暯峴巐曈宍偺懳妏慄偼丆係捀揰偲係拞揰偺偄偢傟偐傪椉抂偲偡傞偡傋偰偺慄暘偵傛偭偰丆俁丗侾丗俀丗俀丗侾丗俁偺斾偵暘妱偝傟傞丏
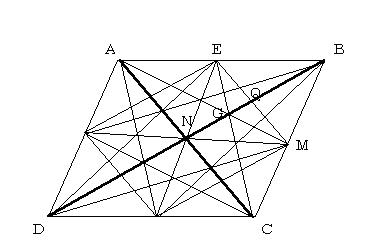
乮徹乯暯峴巐曈宍偺拞慄掕棟偵傛傝丆俛俧亖俀俧俶
俧偼嶰妏宍俤俵俶偺廳怱側偺偱丆俶俧亖俀俧俻
偟偨偑偭偰丆俛俧傪係偲偍偔偲丆俛俻丗俻俧丗俧俶亖俁丗侾丗俀
傛偭偰丆暯峴巐曈宍偺懳妏慄偼捀揰偲拞揰偺偳傟偐傪寢傇慄暘偵傛偭偰丆俁丗侾丗俀丗俀丗侾丗俁偵暘妱偝傟偰偄傞偙偲偵側傞丏
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
2偮愜傝偺曋獬偺懳妏慄偲2偮愜傝偺曋偣傫偺懳妏慄偺岎揰偑5摍暘揰偱偁傞丅
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖





