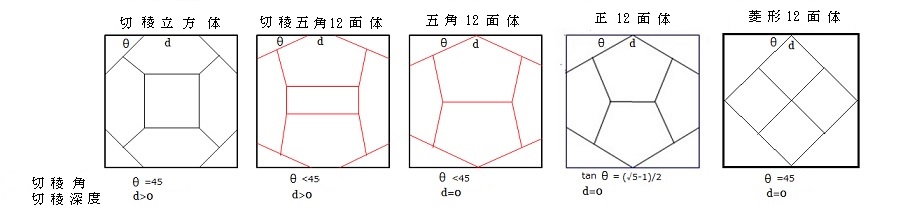
■直観幾何学研究会2023(その26)
切稜立方体の計量
立方体の1辺の長さを2とする。
立方体の表面に残る長方形を2dx2eとする
体積を求めてみたい
===================================
切稜でできる五角形の頂点は
(d,e,1),(1,d,e),(e,1,d)
これらの中間にある頂点はこの3点から等距離にあるので、(D,D,D)とおくことができる。
xy平面上x+by=c上に
(1,d),(e,1),(D,D)があるとすると
1+bd=c
e+b=c
D+bDc
1+bd=e+b
b=(e-1)/(d-1),c=(de-1)/(d-1), D=(de-1)/(d+e-2)
===================================
xz平面上x+bz=c上に(d,1),(1,e)がある
d+b=c
1+be=c
d+b=1+be
b=(d-1)/(e-1),c=(de-1/(e-1)
(0,0)からx+bz=cまでの距離はh=|de-1|/((d-1)^2+(e-1)^2)^1/2
===================================
五角形を2つの台形に分解
S1=1/2・(2d+2D)・{(D-1)^2+((D-e)^2}
S2=1/2・(2e+2D)・{(D-1)^2+((D-d)^2}~
V=12/3・(S1+S2)h+6/3・2d・2e
===================================
検算
正12面体:d=(3-√5)/2,e=0,V=3.41641
菱形12面体:d=0,e=0,v=2
===================================



