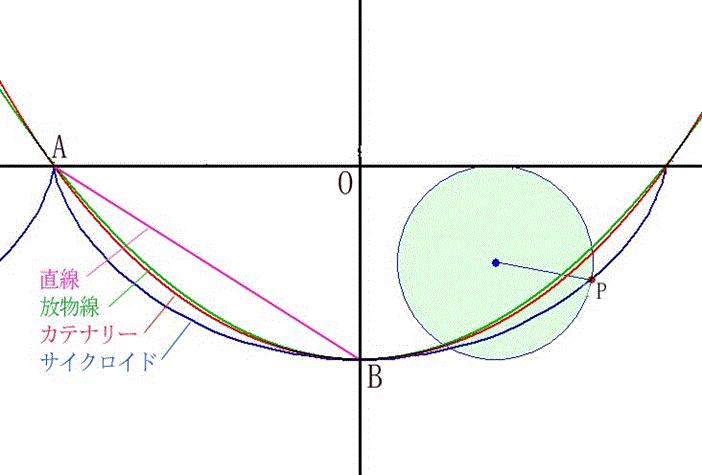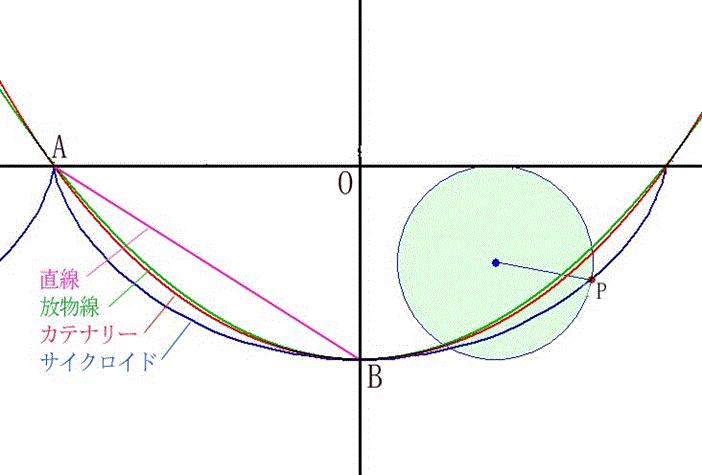重力だけの影響下で、最も速く滑り降りる坂道の形状を求めよ（ガリレオの問題）

1696年、ヨハン・ベルヌーイがこの問題を解き、ヨーロッパ中の優れた数学者への挑戦状として「最速降下線」の問題が提起された。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ガリレオ自身は最速降下線は円弧? と考えていたようであるが、変分学の教えるところによると・・・

最速降下線はサイクロイド (ベルヌーイ)である。

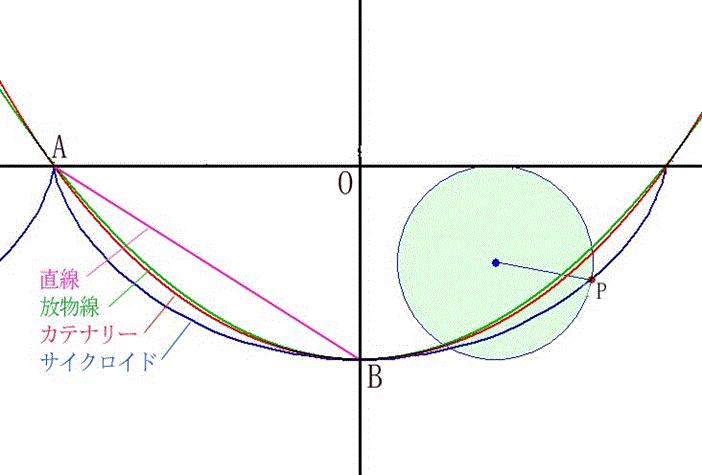
ニュートンは直ちにこれを解き、匿名で解答を送ったが、ベルヌーイはその解法を見てすぐに解答者を知ったという逸話は余りにも有名

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

直線、放物線、サイクロイド、円弧を比べると、サイクロイド、放物線、円弧、直線の順に遅くなります。

長さが一番短い直線が一番遅いのですが、そのため、サイクロイドはスキーのジャンプ台などに使われています。

なお、サイクロイドと直線の間の面積は回転円の半径を１とすると3π、サイクロイド弧の長さは8となります。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝