Vesica Piscisを用いた正五角形の近似的作図法が知られている．コンパスと定規を用いて，正六角形と組み合わせることで，許容内の精確さの正五角形が得られるそうである．計算して確かめてみよう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】近似的な内接正５角形の作図

　円Ｏに内接する近似正５角形の作図の手順は

［１］直径ＡＢを引く

［２］直径ＡＢを５等分し，その等分点を１，２，・・・，４とする

［３］ＡＢを１辺とする正三角形の頂点となる点Ｃを求める

［４］点Ｃと点３を結び，その延長と円が交わる点をＤとする

［５］ＢＤが正５角形の１辺の長さとなる

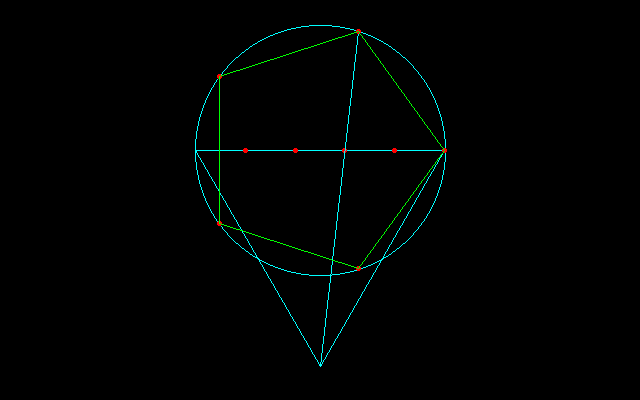
　点Ｃ（−√３，０），点７（１／５，０）を結ぶ直線は

　　ｙ＝５√３・ｘ−√３

ｘ^2＋ｙ^2＝１に代入すると

　　ｘ^2＋７５ｘ^2−３０ｘ＋３＝１

　　３８ｘ^2−１５ｘ＋１＝０

　　ｘ＝（１５＋√７３）／７６＝０．３０９７９

　一方，

　　ｃｏｓ（２π／９）＝０．３０９０１８

と近似度は高いことがわかる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】Vesica Piscisを用いた近似的な内接正５角形の作図

［１］半径が等しく，その中心が互いの円周上にある４円が重なり合った共通部分の両端を点Ａ（−１，０），点Ｂ（１，０）とする．ＡＢが正５角形の１辺の長さとなる．

［２］点Ａを中心とする円を第１円，点Ｂを中心とする円を第２円とする．

［３］第１円と第３円の交点が正六角形の頂点となる．点Ｃ（−２，−√３）とする．

［４］点Ｃと第３円上の点（０，２−√３）を通る直線と第２円の交点を点Ｄとすると，点Ａ，Ｂ，Ｄが正五角形の３頂点となる．

　点Ｃ（−２，−√３），点（０，２−√３）を結ぶ直線は

　　ｙ＝ｘ＋２−√３

（ｘ−１）^2＋ｙ^2＝４に代入すると

　　ｘ^2＋（１−√３）ｘ＋２（１−√３）＝０

　　ｘ＝（√３−１＋√（６√３−４）／２＝１．９００３３

　一方，

　　２ｃｏｓ（π／１０）＝√（２√５＋１０）／２＝１．９０２１１

と近似度は高いことがわかる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】Vesica Piscisを用いた近似的な内接正５角形の作図（その２）

［４］を「点Ｃと第３円上の点（０，２−√３）を通る直線と第４円の交点を点Ｄとすると，点Ａ，Ｂ，Ｄが正五角形の３頂点となる．」としたらどうなるだろうか？

　点Ｃ（−２，−√３），点（０，２−√３）を結ぶ直線は

　　ｙ＝ｘ＋２−√３

　ｘ^2＋（ｙ−√３）^2＝４に代入すると

　　ｘ^2＋（１−√３）ｘ＋２（１−√３）^2−２＝０

　　ｘ＝（√３−１＋√２（√３−１）＝１．９４２０５

となって，近似度が劣化する．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝