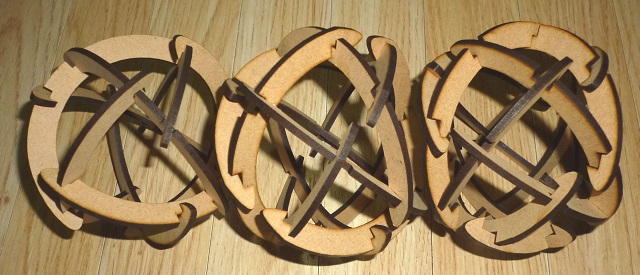正則型ではA+B=πが成り立つが

非正則型ではA+α=πとなる。

さらに、

球面ｎ角形の辺の長さをa,内角をαとする。S=nα-(n-2)π

球面ニ等辺三角形は（π-α、π/2、π/2)であるからT＝π-α

合計はs+nT=2π

3等分では大円にならない

a+α=π,a+b=2/πでなければならない

（その４１）で、cosα=2cos(π/n)-1となったが、以下の結果は変わらない。

N=3 a=90 b=0

N=4 a=65.5302 b=24.4698

N=5 a=51.8273 b=38.1728

N=6 a=42.9415 b=47.0585

N=7 a=36.6884 b=53.3156

N=8 a=32.0313 b=57.9687

N=9 a=28.4317 b=61.5683

N=10 a=25.5628 b=64.7372

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

N＝4の場合の模型を掲げる

N＝6の場合の模型を掲げる

反角柱の側面の三角形が二等辺であることが条件のようなので、それがわかるように４，５，６並べてみました。　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

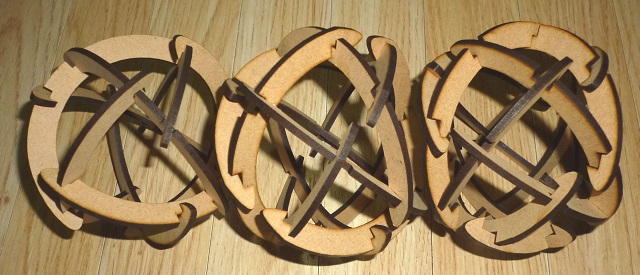
　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝