正三角形２枚、二等辺三角形２枚の四面体

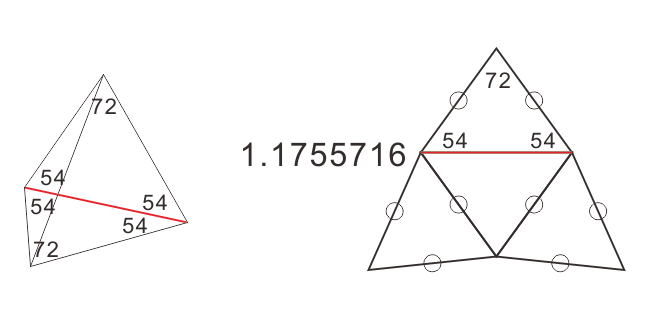
を考える。この四面体を二面角の計算例として取り上げてみたい。

赤い線の二面角は76.3455度であって、72度にはならないのである。

逆に、赤い線の二面角が72度になる二等辺三角形を求めてみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

底面となる二等辺三角形を

A(0,cosx,0)

B(-sinx,0,0)

C(sinx,0,0)

四面体の頂点を

d(0,y,z)

とする。

(y-cosx)^2+z^2=1

(sinx)^2+y^2+z^2=1

を解くと、

z^2=1-(y-cosx)^2

(sinx)^2+y^2+1-(y-cosx)^2=1

2ycosx+(sinx)^2-(cosx)^2=0

2ycosx=cos2x

y=cos2x/2cosx

z^2=1-(cos2x/2cosx-cosx)^2

z^2=1-(cos2x-2(cosx)^2)^2/(2cosx)^2

z^2=1-1/(2cosx)^2

検算しておきたい。

x=36のとき、cosx=τ/2,cos2x=1/2τ

y=1/2τ^2

z^2=1-1/τ^2=τ-1=1/τ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

あとは、各面の法線ベクトルを求めて、それらのなす角を求めればよい。

二等辺三角形の頂角が31.7175x2のとき、二面角は72度となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

31.7175度は、立方体を切稜して正十二面体を作る際の定規の角度ですね。

正十二面体は、空間を埋めようとしても隙間ができますが、その面は頂角がπ/5ｘ２だから平面の５等分の２倍。

他方、５個で隙間なく重五角錐をつくる四面体の表面の二等辺三角形の頂角は、正十二面体の切稜角の２倍。

ちょうど２次元と３次元の数値が置き換わるような関係ですね。これもまた黄金比の不思議の一つでしょうね。

向かいの二面角は何度ですか？　　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝