正三角形２枚、二等辺三角形２枚の四面体

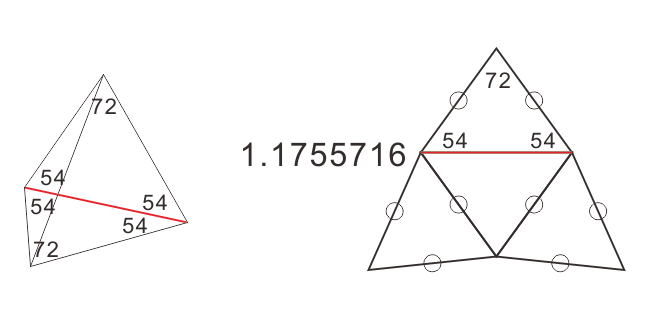
を考える。この四面体を二面角の計算例として取り上げてみたい。

赤い線の二面角は76.3455度であって、72度にはならないのである。

逆に、赤い線の二面角が72度になる二等辺三角形を求めてみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

底面となる二等辺三角形を

A(0,cosx,0)

B(-sinx,0,0)

C(sinx,0,0)

四面体の頂点を

d(0,y,z)

とする。

(y-cosx)^2+z^2=1

(sinx)^2+y^2+z^2=1

を解くと、

z^2=1-(y-cosx)^2

(sinx)^2+y^2+1-(y-cosx)^2=1

2ycosx+(sinx)^2-(cosx)^2=0

2ycosx=cos2x

y=cos2x/2cosx

z^2=1-(cos2x/2cosx-cosx)^2

z^2=1-(cos2x-2(cosx)^2)^2/(2cosx)^2

z^2=1-1/(2cosx)^2

検算しておきたい。

x=36のとき、cosx=τ/2,cos2x=1/2τ

y=1/2τ^2

z^2=1-1/τ^2=τ-1=1/τ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

あとは、各面の法線ベクトルを求めて、それらのなす角を求めればよい。

二等辺三角形の頂角が31.7175x2のとき、二面角は72度となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝