正三角形２枚、二等辺三角形２枚の四面体

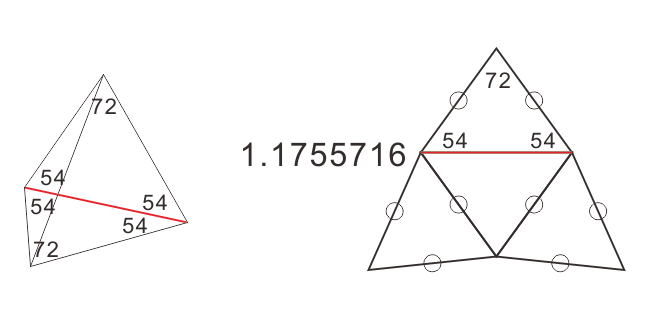
を考える。この四面体を二面角の計算例として取り上げてみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

cos36=τ/2

sin36={(√5)/4τ}^1/2

底面となる二等辺三角形を

A(0,cos36,0)

B(-sin36,0,0)

C(sin36,0,0)

四面体の頂点を

d(0,y,z)

とする。

(y-cos36)^2+z^2=1

(sin36)^2+y^2+z^2=1

を解くと、

y=1/2τ^2

z=1/√τ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

あとは、各面の法線ベクトルを求めて、それらのなす角を求めればよい。

86.4868

65.199

76.3455

となり、72度にはならないのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ］四面体のひとつの頂点に集まる３面の頂角ａ，ｂ，ｃが与えられたとき，３つの二面角α，β，γを定木とコンパスで作図せよ．

［Ｑ］四面体の６辺の長さが与えられている．△ＡＢＣに対する頂点Ｄの高さをを定木とコンパスで作図せよ．

［Ｑ］頂点Ｄから△ＡＢＣに下ろした垂線の足を定木とコンパスで作図せよ．

［Ｑ］ヒルの直角錘ＡＢＣＤをＣＡ，ＣＢ，ＣＤに沿って切り開くと六角形ができる．△ＡＢＤに対する頂点Ｃの高さを定木とコンパスで作図せよ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝