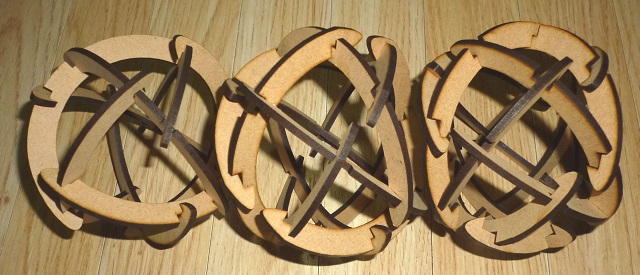球面ｎ角形の辺の長さをa,内角をαとする。S=nα-(n-2)π

球面ニ等辺三角形は（π-α、π/2、π/2)であるからT＝π-α

合計はs+nT=2π

3等分では大円にならない

a+α=π,a+b=2/πでなければならない

（その４１）で、cosα=2cos(π/n)-1となったが、以下の結果は変わらない。

N=3 a=90 b=0

N=4 a=65.5302 b=24.4698

N=5 a=51.8273 b=38.1728

N=6 a=42.9415 b=47.0585

N=7 a=36.6884 b=53.3156

N=8 a=32.0313 b=57.9687

N=9 a=28.4317 b=61.5683

N=10 a=25.5628 b=64.7372

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

N＝4の場合の模型を掲げる

N＝6の場合の模型を掲げる

反角柱の側面の三角形が二等辺であることが条件のようなので、それがわかるように４，５，６並べてみました。　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

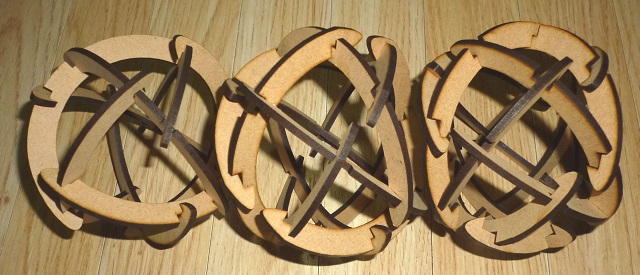
青山学院の西山先生よりお礼状をいただいた。

素敵な立体細工を送っていただきました．ありがとうございます．

一つは大円が正方形を切り出しているもの，もう一つは六角形を切り出しているものでした．実際このようにして手で触れるといろいろ細かいところがわかります．辺が完全な大円で構成されているとよいなと思いましたが，非常に精巧な造りで今ちょうど鑑賞させていただいています．

私が興味があるのは五芒星で，これは（星形の頂点での直交性を保ったまま）辺の長さが比較的自由に変えられるわけです．したがって，大円を可動式にできないのかなぁとむちゃな夢想をしています．木工だと難しそうですね．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

おそらく一番適しているのはCGで、つぎに竹ひごや樹脂のわっかを輪ゴムでとめたものでしょうか。ダヴィンチグリッドは交点を固定しますので不向きだろうと思います。

このｎ芒星のシリーズで、大円(弧）となるのは五芒星だけです。それはなぜなのか、というテーマを学生さんに研究していただくには、３つの模型がひょっとすると役に立つかもしれませんね。　　（中川宏）

　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝