■掛谷の問題(その16)
ところが、掛谷の問題はこれで終わりではなかった・・・
掛谷の問題を星状図形に制限すると、どうなるのだろうか?
星状図形に対する掛谷の問題では、針の回転の可能な星状図形の面積は必ず
π/108以上である
すなわち、ベシコヴィッチ型定理は存在しないのである。
===================================
[1]ペリトロコイド星状図形
長さが1である線分を1回転させることのできるペリトロコイド星状図形の面積は[π/8,π/4)である
すなわち、下限はデルトイドである。
π/8=.392699
===================================
[2]包絡線星状図形
.448431

.411505

.397713
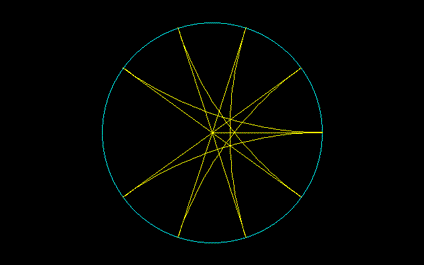
.391406<π/8=.392699

===================================
[3]円弧星状図形
.396782

.316801<π/8=.392699

===================================
星状図形に対する掛谷の問題は未解決で、
現在知られている最適値は(掛谷定数)
(5-2√2)π/24=0.2842582246・・・
===================================








