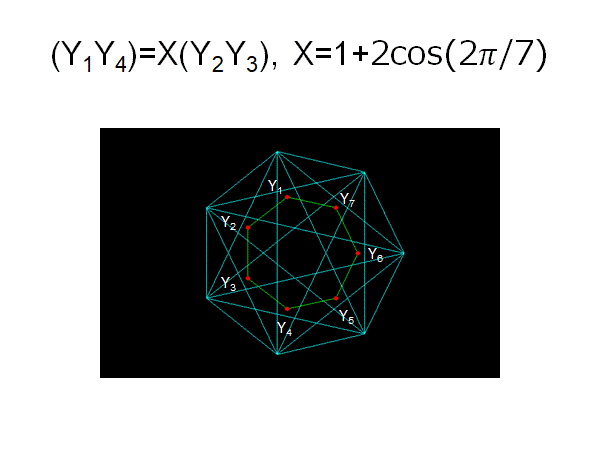この問題のさらなる一般化

[Q}n次元正単体の(n+1)個のファセット上に各1個、 計(n+1)個の点を配置、それらを結んで、 n次元正単体の中心を通る正(n+1)角形を作ることは可能か？

を考えてみると

[定理]n次元正単体のn-1次元面(面数:n+1)のn+1個の定点を通る中心断面上の点を結んで、正n+1角形を無数に構成することができる

[定理]n次元正単体のn-2次元面(面数:n(n+1)/2)のn+1個の定点を通る中心断面上の点を結んで、最大の正n+1角形を構成することができる

が成り立つことが予想される。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

すこし補足しておきたいのであるが、

n+1個の定点をn-1次元面上に置くことは可能であるが、一意には決まらない（不定）

n+1個の定点をn-3次元面上に置くことはできない（不能）

あとはn-2次元面上のn+1個の定点の構成法を示せばよいことになる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正単体の構成

n次元正単体(頂点数:n+1)をn次元空間内で作ると、一般に座標が無理数になる。そこで

n次元正単体を最も手軽に作るには、全体を1次元上げて、(n+1)次元空間内の単位点(n+1)個から生成される単体をとることである

すると1辺は√2 中心は(1/(n+1),・・・,1/(n+1))の正単体が構成される

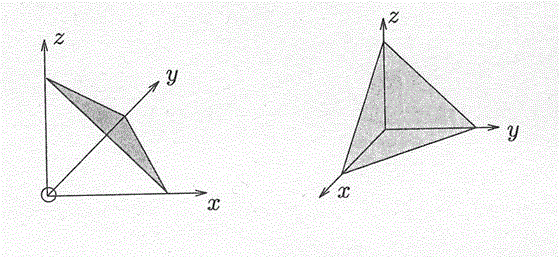
n次元正単体を2次元に投影したとき、その対称性を損なわず、かつ、複数の頂点が重ならないように輪郭が正n+1角形となるように座標軸をとることができる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

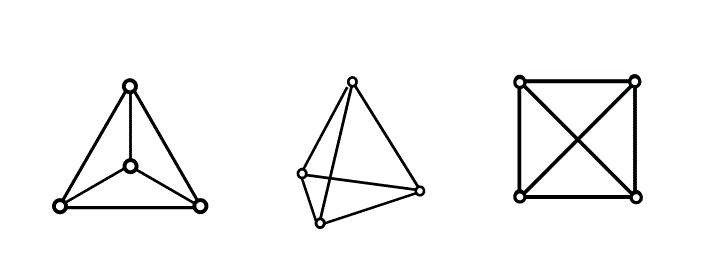
n=6の場合、正七角形にすべての対角線を引いたK7グラフ（水色の図）ができあがる。

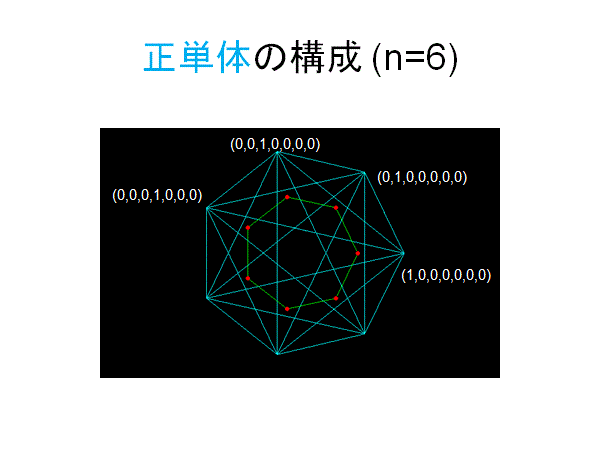
とはいっても、正n+1角形の頂点の構成法を解説するのは難しい(図の赤い点）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

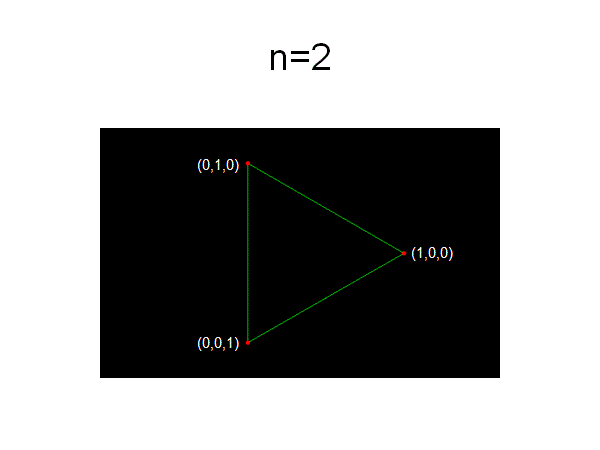
n=2からn=6までの頂点を掲げる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
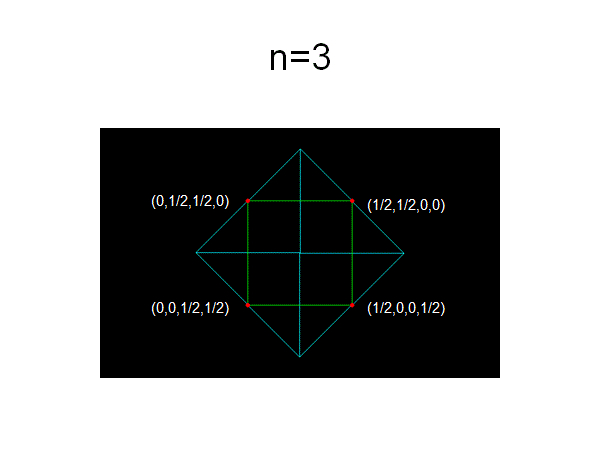
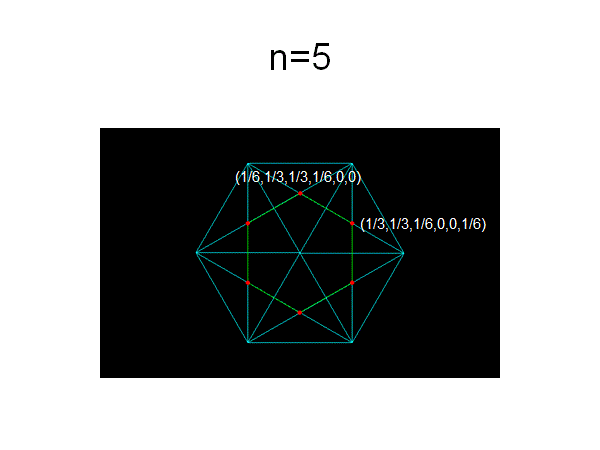
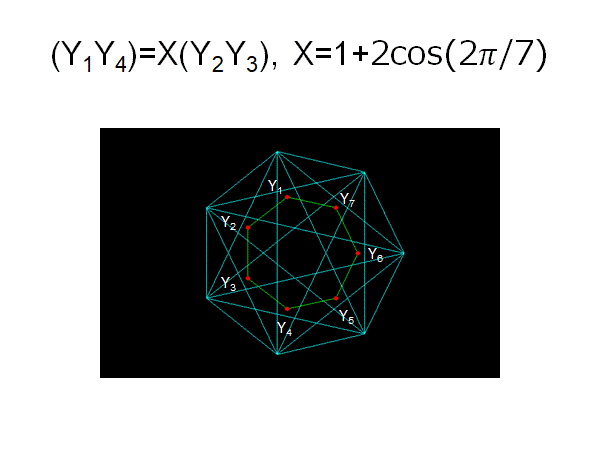