[Q]正四面体の4面上に各1個、 計4個の点を配置、それらを結んで、四角形を作る

ただし、四角形は正方形であり、かつ、正四面体の中心を通らなければならない

[A]

正四面体の6辺中、4辺の中点を通る中心断面は正方形になる

正四面体の4面上の4個の点を結んで、正方形を無数に構成することができる

4点が正四面体の辺の中点上にあるとき、正方形は最大になる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

それでは、この問題の高次元版

[Q}4次元正5胞体の5胞上に各1個、 計5個の点を配置.それらを結んで、正5胞体の中心を通る正五角形を作ることは可能か？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

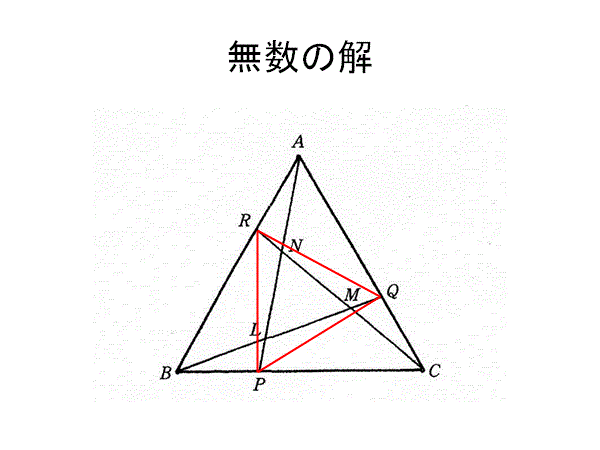
逆に2次元版を考えると

正三角形の3辺上の3個の点を結んで、正三角形を無数に構成することができる

3点が正三角形の辺の中点上にあるとき、正三角形は最小になる

3点が正三角形の頂点上にあるとき、正三角形は最大になる

ことがわかるだろう

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝