（Ｑ）固定された大円（半径Ｒ）の内部に半径がｒ＝Ｒ／３のもう一つの小円が入っているとする．小さい円が大きい円に内接し滑ることなく大きい円に沿って回転すると，動円上の定点はどのような軌跡を描くか？

　（Ａ）一般に、固定された大円（半径Ｒ）の内部に半径ｒ（＜Ｒ）の小円が入っているとする．小さい円（動円）が大きい円（定円）に内接し滑ることなく大きい円に沿って回転すると，動円上の定点はハイポサイクロイドを描く。

　　　　ｒ＝Ｒ/3の場合、デルトイドを描く

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[１]固定された大円（半径Ｒ）の内部に半径がｒ＝２Ｒ／３の中円が入っているとする．中円が大きい円に内接し滑ることなく大きい円に沿って回転すると，動円上の定点はどのような軌跡を描くか？

プログラムを作って確かめてみると、デルトイドを描くは正しい。中円が大きい円に内接し滑ることなく大きい円に沿って回転していることになる。

[３]中円（半径2ｒ）の内部に半径ｒの小円が入っているとする．中円（動円）が固定された小さい円（定円）に接しながら回転すると，動円上の定点の軌跡はデルトイドを描くように見える。プログラムを作って確かめてみると、デルトイドを描くは正しい。「滑り」を生じていないことになる。

[２]固定された小円（半径ｒ）に外接して半径がｒの小円がある．この動円が固定円に外接し滑ることなく固定円に沿って回転すると，動円上の定点の軌跡はカージオイドを描くはずである。デルトイドを描くように見えるのは「滑り」を生じているからだと考えられる。

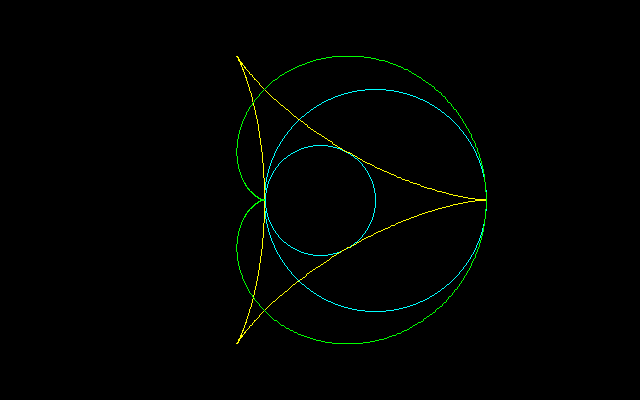
よく見ると動円はカージオイドの場合と逆回転している。以下の図は逆回転するとカージオイドを描くことを示している。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝