【１】ポンスレーの定理

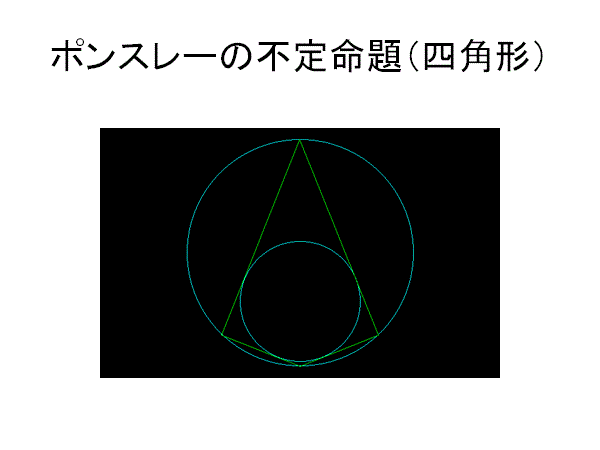
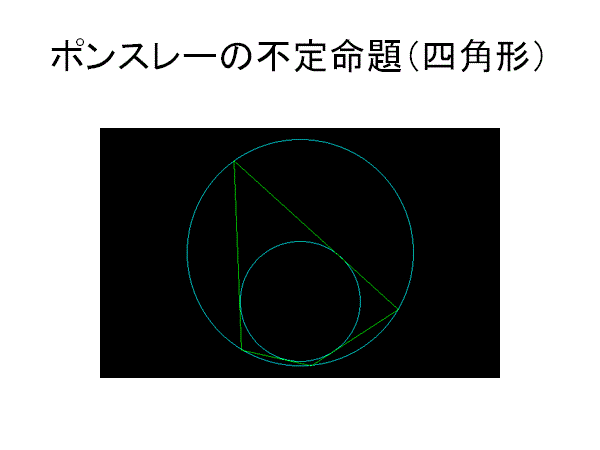
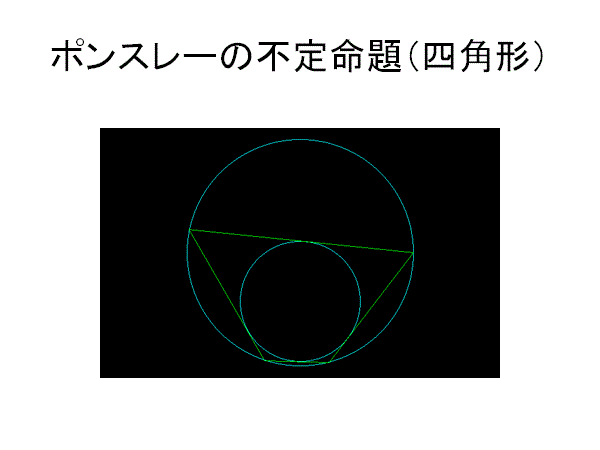
小円を大円の内部におく．大円上の点Ｐ0から小円へ接線を引き，大円と交わる点をＰ1とする．Ｐ1から再び小円へ接線を引き，大円と交わる点をＰ2とする．この２つの円の中間に次々に接する接線列を作る．たいていの場合，最後の交点は最初の点Ｐ0と重ならない．しかしときとして完全に重なる場合がある．このとき，最初の点Ｐ0をどこに選ぼうとも完全な多角形環をなす．

シュタイナーの定理とポンスレーの定理，２つの定理は円鎖が閉じるか接線多角形が閉じるかの違いだけで，内容的には類似した定理に感じられるかもしれない．しかし，シュタイナーの定理は円を円に写すメビウス変換ｗ＝（ａｚ＋ｂ）／（ｃｚ＋ｄ）により同心円の場合に帰着させて証明できるのに対して，ポンスレーの定理では直線を直線に移す円板の非ユークリッド幾何学的な変換が必要になるが，それは

　　ｘ’＝（ａｘ＋ｂｙ＋ｃ）／（ｕｘ＋ｖｙ＋ｗ）

　　ｙ’＝（ｄｘ＋ｅｙ＋ｆ）／（ｕｘ＋ｖｙ＋ｗ）

という形の（実）変換である．その意味で 2つの定理は似て非なるものである．また，シュタイナーの定理の基底は2次式であったが，ポンスレーの定理では高次式になる．その意味では後者のほうが本質的に難問である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

なお、ポンスレーの定理は2つの円を2つの楕円の置き換えても正しい

楕円と楕円の組み合わせで証明されている

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

同心円でない場合

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝