アステロイドの平行曲線

x=2(cost)^3 - 3sint

y=2(sint)^3 - 3cost

は、特異点をもたずに正三角形に内接しながら回転することができる円以外の内転形である。中心軌道は円となる。

一般に、アステロイドの平行曲線

x=w1(cost)^3 +w2sint

y=w1(sint)^3 +w2cost

は、荷重比|w1/ｗ2|が相対的に大きくなるとアステロイドに、小さくなると円に近づく。どんな定幅図形や内転形も円弧多角形から構成されているものと誤解してはならない。円弧でない内転形(中心軌道は円) が存在する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

x=2(cost)^3-3sint, y=2(sint)^3-3cost

x=(cost)^3-3sint, y=(sint)^3-3cost

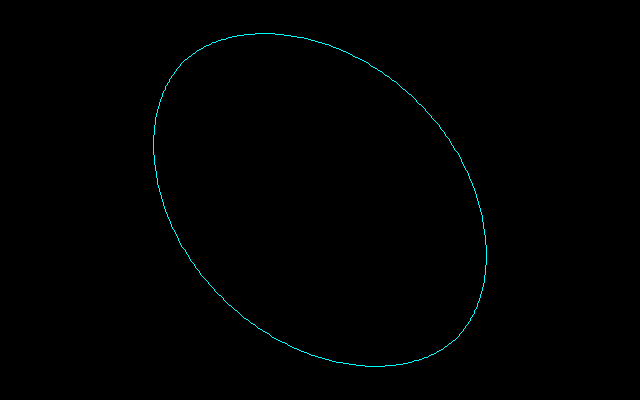
x=.5(cost)^3-3sint, y=.5(sint)^3-3cost

x=.1(cost)^3-3sint, y=.1(sint)^3-3cost

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝