有名な掛谷の問題は長さが１である線分を１回転させるのに必要な最小面積図形の問題であるが，藤原の論文にある卵形線の最大最小問題からその極限形として自然に生じた線分問題であって，正多角形の内転形（凸多角形の各辺に接しながらその中で１回転できる卵形線）の考えに負うところが大きいとされる[1][2]．

[Q] 正三角形に内接しながら回転することができる円以外の図形は何か?（藤原松三郎の問題）

[A]ルーローの円弧二角形，藤原・掛谷の円弧二角形，アステロイドの平行曲線 (非円弧二角形)．すべての定幅曲線の周長は等しい（バービエ）・定幅曲線のなかで面積が最大になるのは円，最小になるのはルーローの三角形である（ブラシュケ，ルベーグ）に対して，正多角形のすべての内転形の周長は等しい・正三角形の内転形で面積最小のものは藤原・掛谷の二角形である，などは藤原による内転形定理である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

参考文献

[1] Fujiwara M.: Ueber die einem vielecke eingeschriebenen und umdrehbaren konvexen geshhlosenen Kurben, Science reports, Sendai, 4 (1915), 43-55

[2]Fujiwara M., Kakeya S.: On some Problems of Maxima and Minima for the Curve of Constant Breadth and the In-revolvable Curve of Equilateral Triangle, Tohoku Math. J. 11(1917), 92-110.

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ルーローの円弧二角形

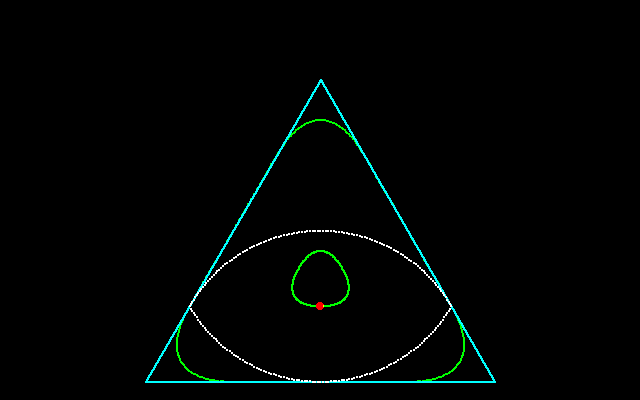
藤原・掛谷の円弧二角形

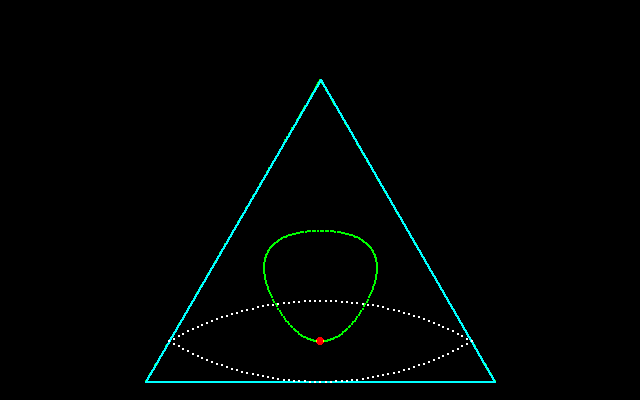
アステロイドの平行曲線 (非円弧二角形)．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
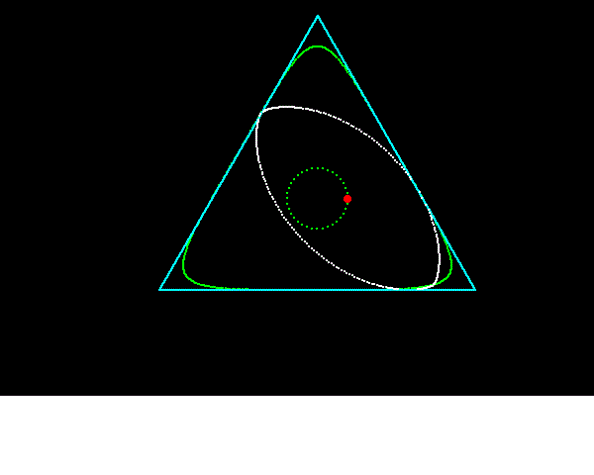