■メルカトール図法(その2)
ランベルトの正積円筒図法
円柱の容器の中にテニスボールが1個入っている。ボールの表面を円柱の表面に投影し、円柱を切って開くとボールの平面投影図が得られる。
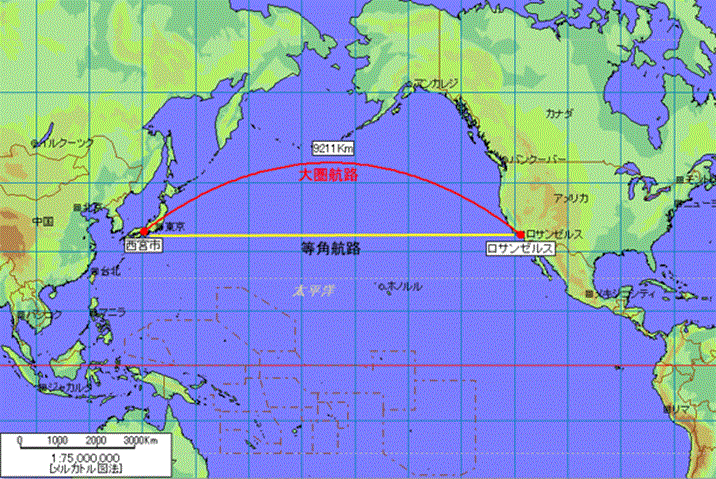
しかし、この地図では大円コースにはならないし、等角航路(航程線)にもならない。角度が変化してしまうからである。
===================================
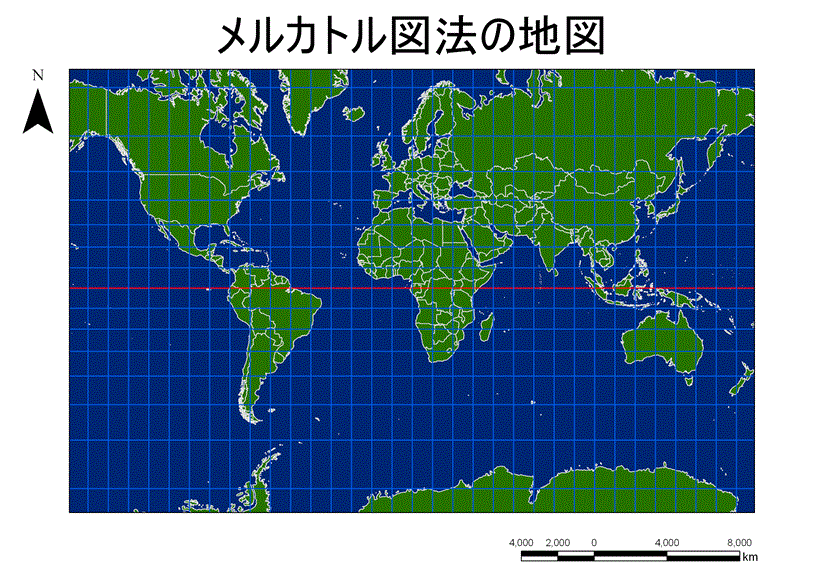
メルカトール図法
角度を保存する図法を正角図法という。正角図法で2点を結ぶ線は大円の弧ではなく、等角航路になる。
メルカトールの地図には平面図法の性質が遺伝するので,正距図法とはならない.すなわち,地図上の任意の2つの点を結ぶ線分は測地線ではない.また,logがついている分,高緯度における歪みは円筒図法ほど誇張されにくいと思われるが,それでもグリーンランドは南アメリカより大きく表される(実際は1/9の大きさである).
===================================
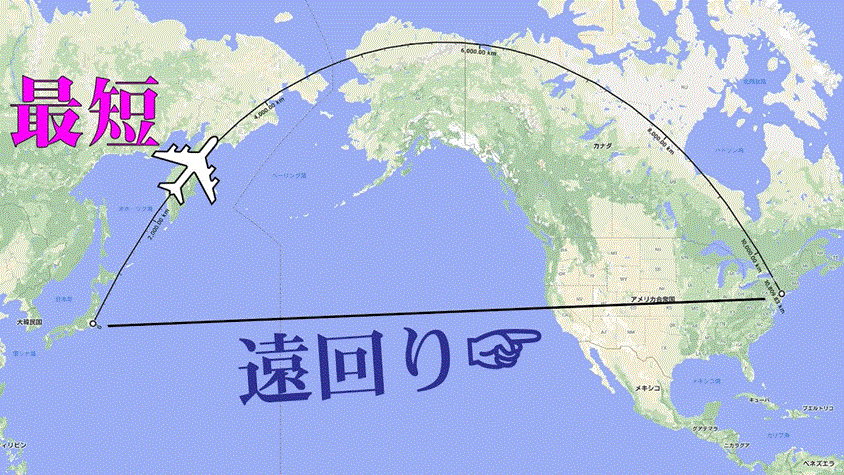
正距図法
2点を結ぶ線が実際の最短経路になる投影図法
===================================






