パウル・シャッツ環・ヨハネス・シェンケ環の仲間たちを紹介したい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

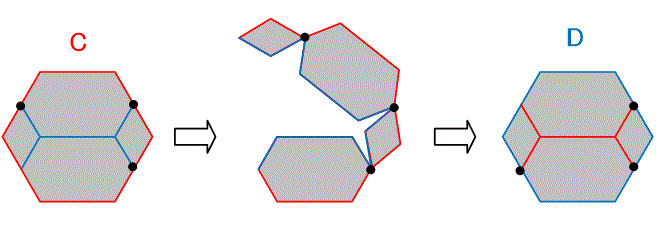
【１】エンドレス・キューブ

立方体を２×２×２に８等分する．８個の小立方体を８カ所で繋げる．連結の位置関係は実におもしろく，そのように繋げばバラバラになることなしに，６面×８個＝４８面すべてをみせることができる．たとえば，表面２４個にロンドンの観光写真を載せれば，裏面（隠れている面）２４個にパリの観光写真を載せることができるのである．

表の２４面を裏返すと裏の２４面が現れてくることを利用して観光地の写真を貼り付けてあるおみやげグッズもある．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】エンドレスキューブのつなぎ方

　直交３方向を東西・南北・天地方向にとる．天面の東西方向の２カ所を繋げる．東面・西面の南北方向の２カ所ずつ，計４カ所を繋げる．南面・北面の天地方向の底面よりを１カ所ずつ，計２カ所を繋げる．底面はそのままにする．

　これで，８個の小立方体を８カ所で繋げたことになる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

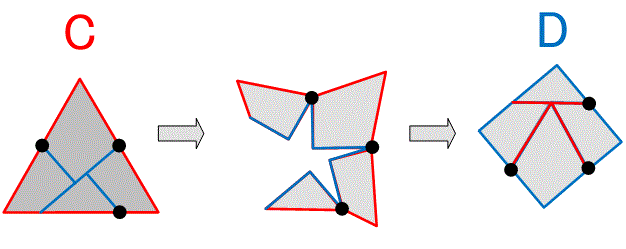
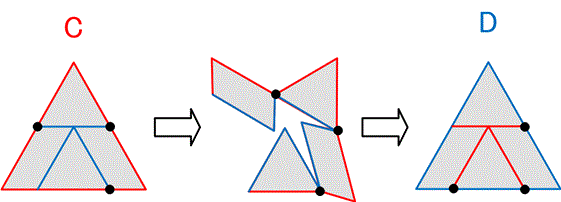
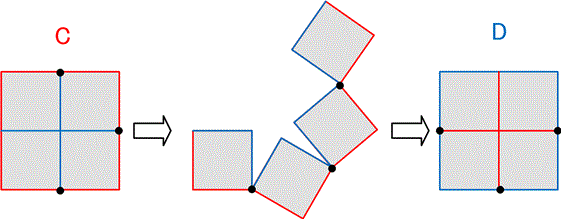
【３】カンタベリー・パズル

　パズル作家デュドニーが１９０２年に見つけたとされる．正三角形を正方形に（正方形を正三角形に）する４片裏返しなしの有名なパズルであり，ヒンジで４片を回転させて正三角形と正方形を相互変換させる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝