周長Lが一定の平面図形のなかで、面積Sが最大のものは円であることが、シュタイナー対称化により直感的に理解することができる。

しかし、それでは厳密な証明にはなっていない。

フルヴィッツが20世紀初頭に発表した有名な論文[2]にはフーリエ級数を用いた等周問題の厳密な証明のほか，アステロイドの平行曲線は正三角形の内転形であること，デルトイドの平行曲線が定幅曲線（平行な支持線間の距離が一定な卵形線）であることなどが証明されている．この論文からの刺激をうけて，藤原松三郎は一般的な凸多角形の内転形についてフーリエ級数論を応用して解析的に研究した[3]．

[2] Hurwitz A.: Sur quelques applications geometriques des series de Fourier Annales scientifiques de l'Ecole Normale Superieure, Serie 3, Tome 19(1902), pp. 357-408.

[3] Fujiwara M.: Ueber die einem vielecke eingeschriebenen und umdrehbaren konvexen geshhlosenen Kurben, Science reports, Sendai, 4 (1915), 43-55

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

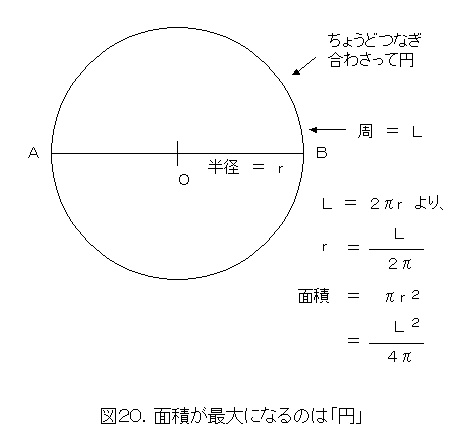
1. 周長Lが一定の平面図形のなかで、面積Sが最大のものは円である。

L2≧4πS (等周不等式)

2. x=a0+a1cost+b1sint

y=c0+b1cost-a1sint

それは点(a0,c0)を中心とする円の方程式である

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

3. アステロイドの平行曲線

x=2(cost)^3 - 3sint

y=2(sint)^3 - 3cost

は、特異点をもたずに正三角形に内接しながら回転することができる円以外の内転形である。中心軌道は円となる。

4. アステロイドの平行曲線

x=w1(cost)^3 +w2sint

y=w1(sint)^3 +w2cost

は、荷重比|w1/ｗ2|が相対的に大きくなるとアステロイドに、小さくなると円に近づく。どんな定幅図形や内転形も円弧多角形から構成されているものと誤解してはならない。円弧でない内転形(中心軌道は円) が存在する。

5. 正五角形の内転形となる円弧四角形は存在しないことが証明されている。

6. しかし、フルヴィッツのフーリエ級数論は、正五角形、正六角形、・・・にも応用できる。

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝