ここでは複素数（円分多項式）を使わずに正五角形が作図可能であることを証明する(別法)

作図可能であることを示すためには２次方程式に帰着することを証明すればよい（作図方法を見つける必要はない）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

定理1

正ｎ角形が単位円（半径１の円）に内接しているとき

１．ひとつの頂点から他のｎ−１個の頂点までの距離の平方和は２ｎに等しい

同義＝すべての２頂点間の距離の平方和はｎ2に等しい

定理２

正ｎ角形が単位円（半径１の円）に内接しているとき

２．ひとつの頂点から他のｎ−１個の頂点までの距離の積はｎに等しい

同義＝すべての２頂点間の距離の積はｎn/2に等しい

別法

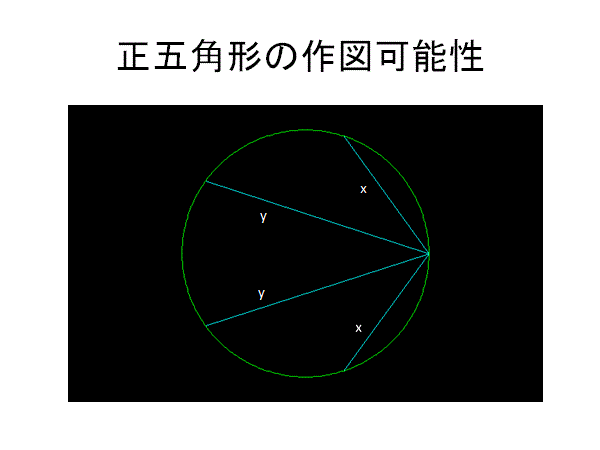
定理１より、2x^2+2y^2=10→ x^2+y^2=5

定理２より、x^2y^2=5

プトレマイオス（トレミー）の定理より、x^2+ｘｙ=y^2

x^2,y^2は連立方程式

x^2+y^2=5, x^2-y^2=-√5

の２実根である

x^2=(5-√5)/2, y^2=(5+√5)/2

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝