Boerdijkはらせんの頂点に同じ大きさの球を配置した円筒内球充填の問題を考察している 。この構造では局所的には最も効率よく最密充填構造を作ることができる。

液晶ディスプレイでは、液晶分子が角柱相とらせん相の間を交代的に遷移する。予期せぬ出来事であったが、このらせんはimage display electronicsへの応用をもっていた。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】液晶ディスプレイの原理

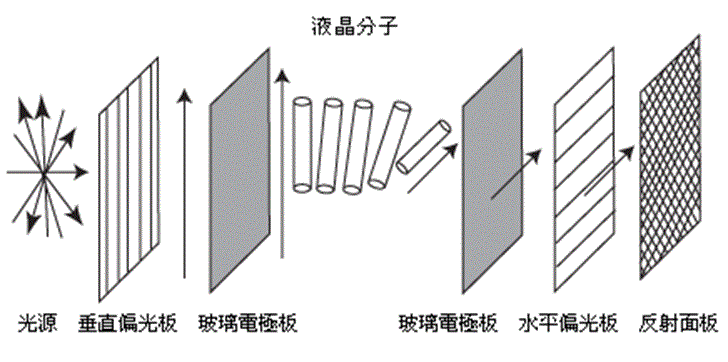
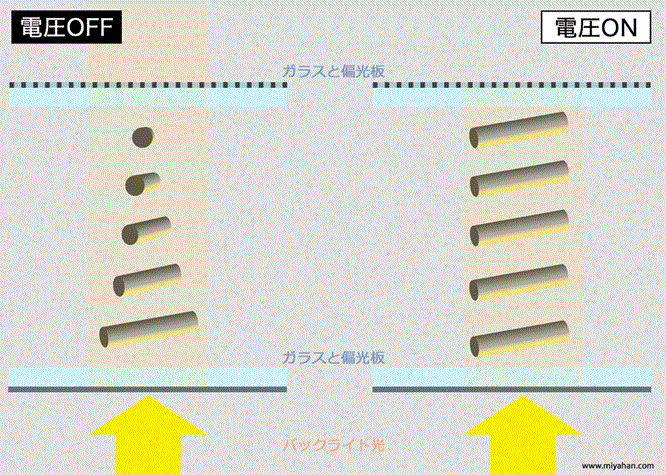
すなわち、液晶分子は第3の偏光板の役割を担っている。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】らせん相(Boerdijk-Coxeterらせん)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】プリズム相 (Sommervilleの等面四面体)

Sommervilleの四面体は3辺の長さ[2,√3,√3]の合同な二等辺三角形4枚からなる等面四面体である．

この四面体には自己複製的な空間充填性が備わっていて，積み上げると正三角柱を作ることができる．

この問題はA群無限鏡映群の問題である

Sommerville三角柱の長さ2の対向する2辺が√3に短縮すると，正四面体が面と面を接合して正三角形面よりなるねじれた柱に変形する．円筒に内接するこの構造体はBoerdijk-Coxeter helixと呼ばれ，ねじれ角arccos(-2/3)=131.8°はこの非等長変換によってもたらされる．その際，辺の長さとねじれ角の大きさの間には美しい変換式が成立する．

このことから、ＢＣらせん柱とSommerville三角柱は相遷移の兄弟分、カウンターパートの関係にあると考えられる。

液晶ディスプレイはこれら二相間の相転移と考えられる。数学的な定式化をすると

[Q]非等長変換の不変式を求めよ

ということになる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【４】練習問題

サマーヴィルの等面四面体は外心・内心・重心が一致するなどの幾何学的性質をもっている。また、相対する辺の長さが等しく、６辺は直方体に内接する。逆にいうと、直方体の頂点を結べば等面四面体が出来上がる。これらの性質を利用して、体積を求めることができるが、発展性を欠くので、ここではオイラーの4面体公式を使って問題に答えることにする

[Q]サマーヴィルの等面四面体（3辺の長さが２,√3,√3の等面四面体）の体積を求めよ

[Q]3辺の長さが1,b,1の等面四面体の体積が最大となるbの値は?

[Q]サマーヴィルの等面四面体（3辺の長さが２,√3,√3の等面四面体）と1辺の長さが√3の正四面体の高さを比較せよ

[Q]3辺の長さが1,b,1の等面四面体の高さが最大となるbの値は?

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝