[Q]それぞれの円の直径を求めよ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

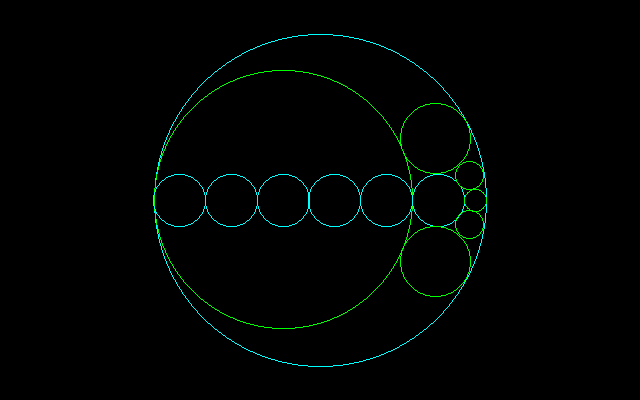
外接円の半径:R

内接円の半径:r

外接円と内接円の中心間距離:d

s=(1-sin(π/n))/(1+sin(π/n))

とおく

2次同次式: d^2=R^2-Rr(s+1/s)+r^2

=(R-rs)(R-r/s)が成り立つ

同心円の場合、r/R=s, R(1-sin(π/n)) =r(1+sin(π/n))でr/Rは最大となる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この問題は、

2次同次式: d^2=R^2-Rr(s+1/s)+r^2

だけでは解けません。

n=6 → s+1/s=10/3

R=1

R+d-r=10r→ d=11r-1

d^2=1-10/3・r+r^2に代入 → r=7/45,d=32/45

R-d-r=1-32/45-7/45=6/45 (甲円の直径)

R+d-r=10r=70/45 (丁), 2r=14/45 (戊)

14/81 (乙), 14/33 (丙） ← メビウス変換

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝