和算は日本特有の数学であるが，和算固有の西洋算とは違ったセンスが必要になる．科学とのつながりがなかったといえばそれまでですが、数学の難しさを楽しむ心・遊び心にあふれていて、日本の数学愛好家たちは楽しみのための数学の発展に努め、自分たちの問題が実用上の応用をもたないことを誇りあることとさえ考えていたのかもしれません。

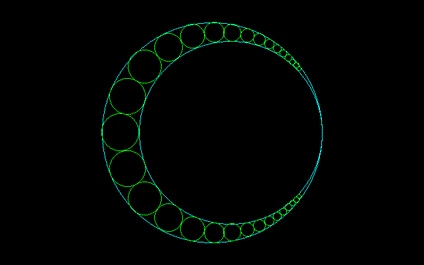
ここでとりあげる和算の問題は大きな円のなかに複数の円を内接させ，それぞれの直径を求める問題である。算額の美しさを鑑賞してみることにしよう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[Q]外円の直径が６寸、甲円の直径が２寸のとき、乙円・丙円・丁円の直径を求めよ

1830年、一関の和算家・千葉秀胤編集「算法新書」の問題を改題

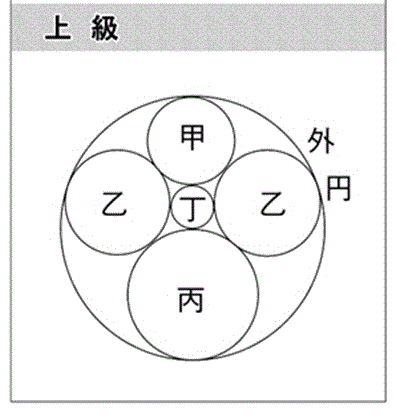
安島直円(1784)など和算家たちは非同心円の高度な問題を取り扱っている。彼らは、シュタイナーの定理(1826)以前に、同様の結論を知っていたことになる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

シュタイナーの不定命題とは、

小円を大円の内部におき，この２つの円の中間に次々に接する円列を作る．たいていの場合，最後の円は重なってしまい，この円列は互いに接する円環をなさない．しかしときとして完全な円環をなす場合がある．このとき，最初の円をどこに選ぼうとも完全な円環をなす．

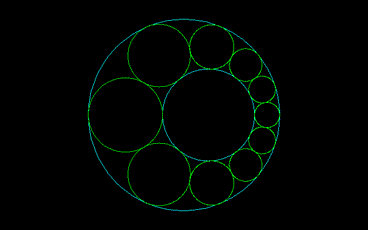
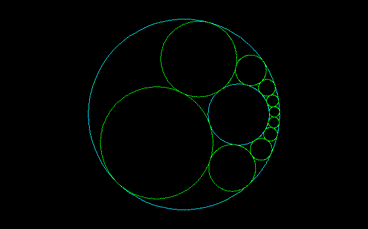
最後の円が最初の円とうまく接するならば、最初の円をどこから始めたとしても円鎖は閉じる

鎖を構成する円の中心はすべてひとつの楕円上にある

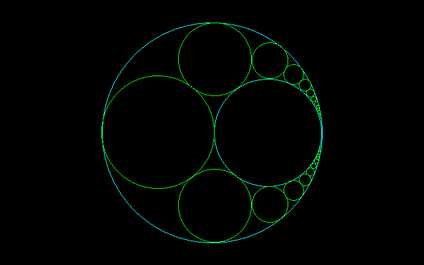
シュタイナーの定理において、n→∞の場合がアルキメデスのアルベロスである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝