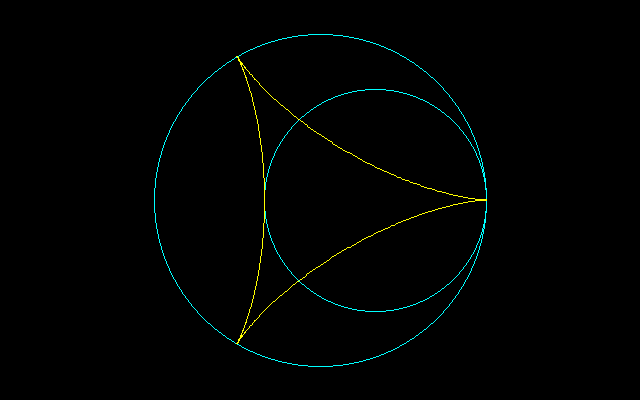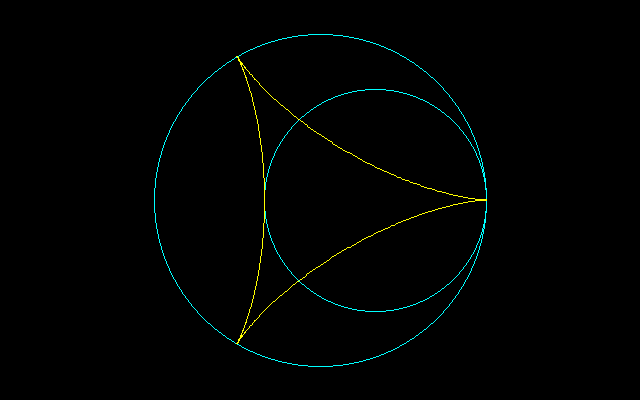コペルニクスの問題とは

半径1の大円に内接して回転する半径1/2の小円の周上の点が描く軌跡は？

というものである。答えは大円の直径上を直線運動するというものである。

それでは、その逆問題

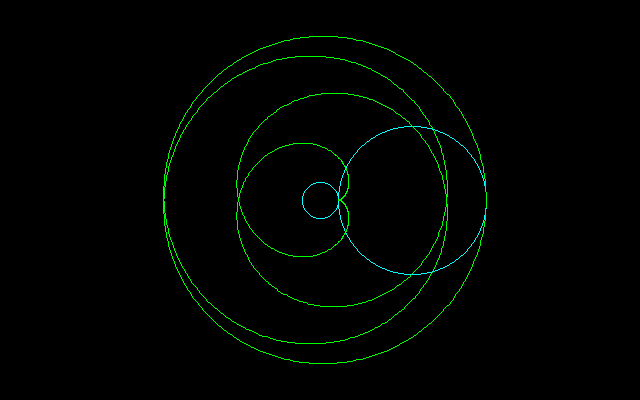
半径1/2の小円に外接して回転する半径1の大円の周上の点が描く軌跡はどのようなペリトロコイド曲線になるか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

答えは、大円の回転方向によって異なるのであるが、

デルトイドは（ハイポサイクロイドかつ）周上の点が描くペリトロコイド

カージオイドは（エピサイクロイドかつ）周上の点が描くペリトロコイド

で、これらは共役なペリトロコイドになっている。

大円の直径はこれらのペリトロコイドの3点接触型内転形になっていることがわかる。

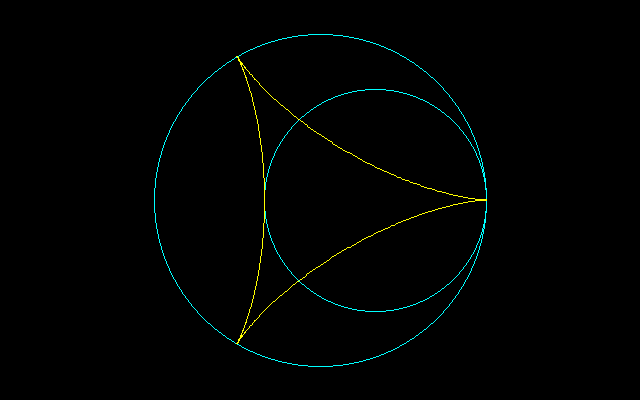
一般に

星状図形は（ハイポサイクロイドかつ）周上の点が描くペリトロコイド

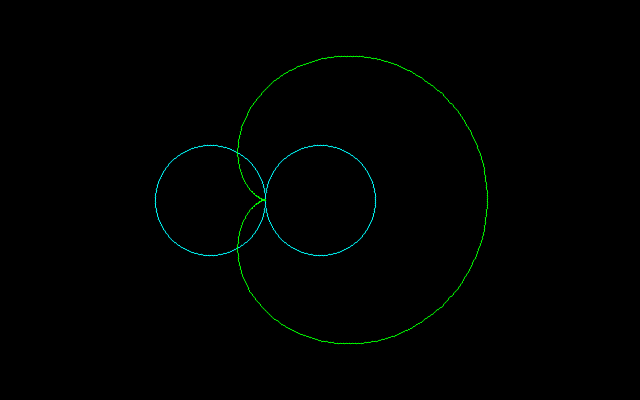
フープ図形は（エピサイクロイドかつ）周上の点が描くペリトロコイド で、とくにペリトロコイド星状図形は回転円の直径を内包していることに留意されたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝