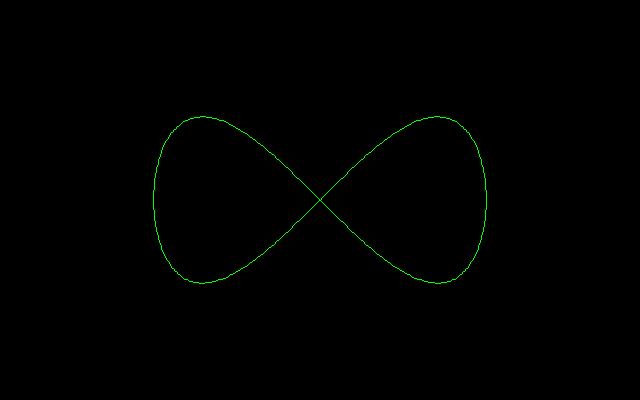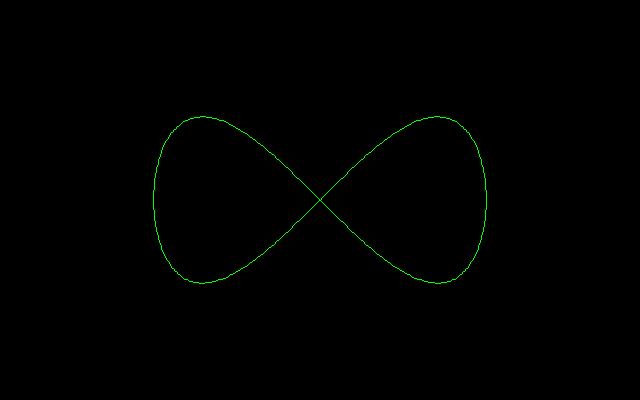単振動の合成はリサージュ図形

x=a・cos(αt)

y=ｂ・sin(βt)

ですが、ゲロンのレムニスケート

x=cos(t)

y=1/2・sin(2t)

y^2=x^2-x^4　

はその例です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

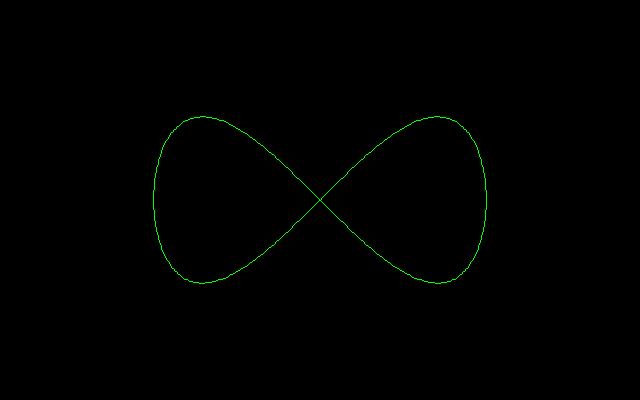
一方、回転運動の合成はエピサイクリック (広義)で、

x=a・cos(αt) + b・cos(βt)

y=a・sin(αt) + b・sin(βt)

複素超越表現すると、

z=a・exp(iαt) + b・exp(iβt)

と表されます。

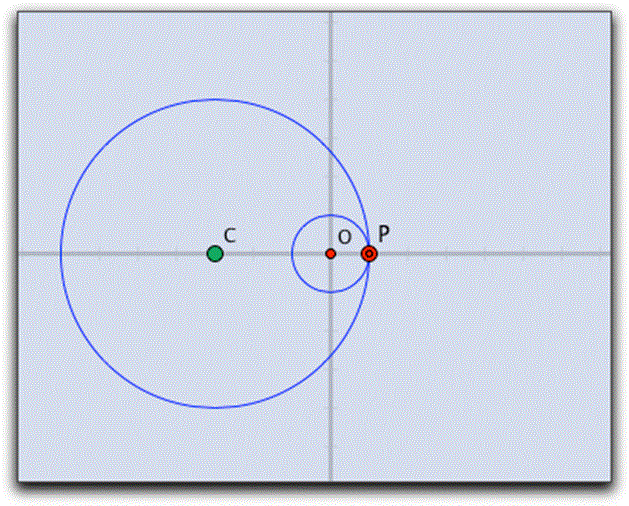
原点を中心とする半径aの円の円周上を等速αで公転する点があり、その点の周りを半径b・等速βで自転する点の軌跡

α/βが有理数のとき、周期運動

エピサイクロイド・ハイポサイクロイド

エピトロコイド・ハイポトロコイド

ペリトロコイドはすべてこの範疇に属する

スピログラフ

スピログラフはイギリスの発明家フィッシャーによって考案されたおもちゃで、大きな歯車型の穴の内側に小さな歯車が回るようになっていて、

この小さな歯車の内側にある空いた穴に鉛筆を差し込んで、歯車を転がすことで模様を描くことができる。

転がす歯車の大きさやペン先を入れる穴の位置によって模様は大きく変化する。これによって描かれる図形はハイポトロコイドである。　　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ギリシア時代の天文学では，神秘的であるべきすべての天体の運動は円とその組み合わせによって支配される（周転円説・エピサイクル）という思想があり，惑星は地球の周りを等速円運動すると考えられていました．神の創造した世界は完全な調和の世界であり，完全なる図形である円こそが神の世界にふさわしいとされたのです

フーリエが波や振動を正弦曲線に分解できると考えたと同様に，古代ギリシア人は惑星運行の連続かつ閉軌道はすべて周転円（エピサイクル）を使って記述することができると考えたというわけです．

ここでは、ハイポサイクロイドの回転円が固定円よりも大きくなった場合(ペリトロコイド)を中心として考えることにします。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
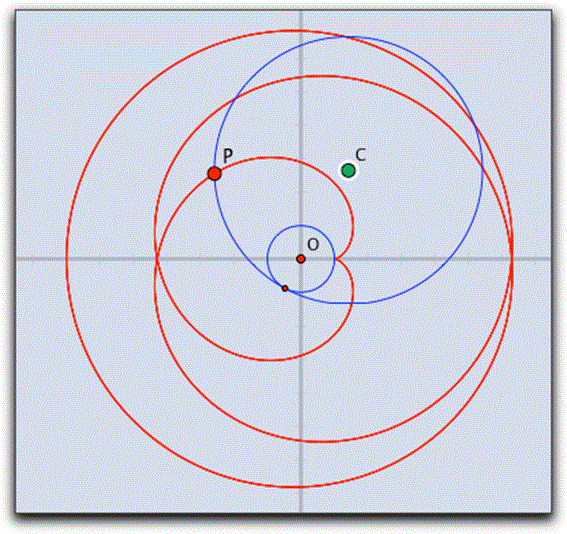