フルヴィッツのフーリエ級数論では等周問題

1. 周長Lが一定の平面図形のなかで、面積Sが最大のものは円である。

L2≧4πS (等周不等式)

2. x=a0+a1cost+b1sint

y=c0+b1cost-a1sint

は点(a0,c0)を中心とする円の方程式である

が論じられていますが、それ以外の話題として正多角形の内転形が取り上げられています。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

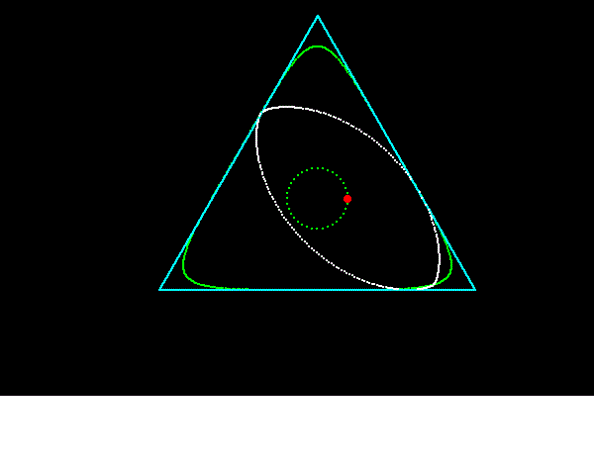
[1]フルヴィッツの二角形

ルーローの二角形と比較すると、非円弧内転形ですが、中心軌道は真円です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正三角形を偏心回転させて、その包絡線を描くと特異点を生じますが、うまく特異点を解消すると、正三角形の内転形が得られます。

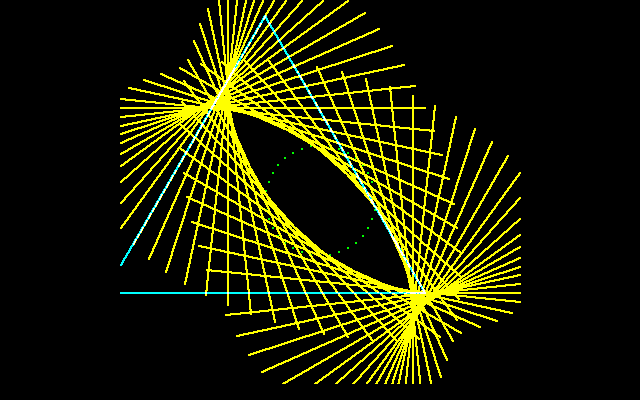
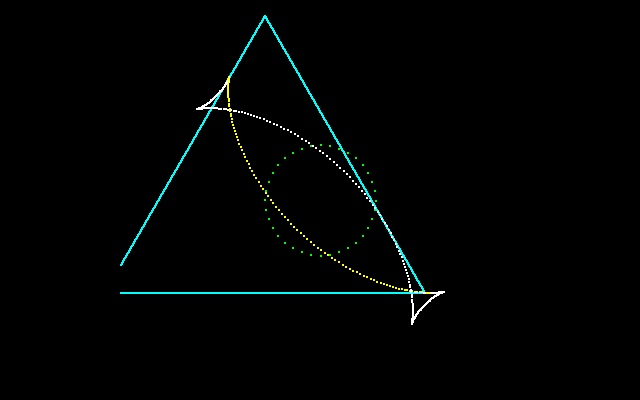
3. アステロイドの平行曲線

x=2(cost)^3 - 3sint

y=2(sint)^3 - 3cost

は、特異点をもたずに正三角形に内接しながら回転することができる円以外の内転形である。中心軌道は円となる。

4. アステロイドの平行曲線

x=w1(cost)^3 +w2sint

y=w1(sint)^3 +w2cost

は、荷重比|w1/ｗ2|が相対的に大きくなるとアステロイドに、小さくなると円に近づく。どんな定幅図形や内転形も円弧多角形から構成されているものと誤解してはならない。円弧でない内転形(中心軌道は円) が存在する。

5. 正五角形の内転形となる円弧四角形は存在しないことが証明されている。

6. しかし、フルヴィッツのフーリエ級数論は、正五角形、正六角形、・・・にも応用できる。

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

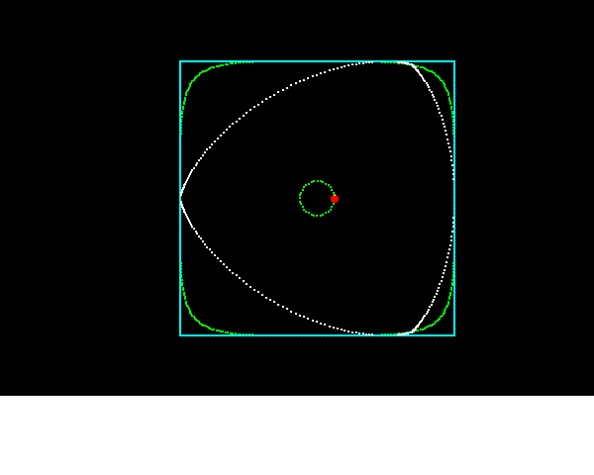
[2]フルヴィッツの三角角形

ルーローの三角形と比較すると、非円弧内転形ですが、中心軌道は真円です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝