以前，単位円の周りの６０本の釘を均等に打ち，釘に糸をかけて正三角形，正方形，正五角形，正六角形を作り．ずべての辺と対角線の長さの２乗和を求めさせる授業を行ったことがある．

　一般に正ｎ角形のずべての辺と対角線の長さの２乗和はｎ^2となる．実際には作れなかったが，正６０角形では３６００になる．平面に限らず，ｍ次元空間でも，単位球の中心に重心がある頂点数ｎの多胞体ではずべての辺と対角線の長さの２乗和はｎ^2となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　［参］大関清太「数の森」里文出版，ｐ１１４

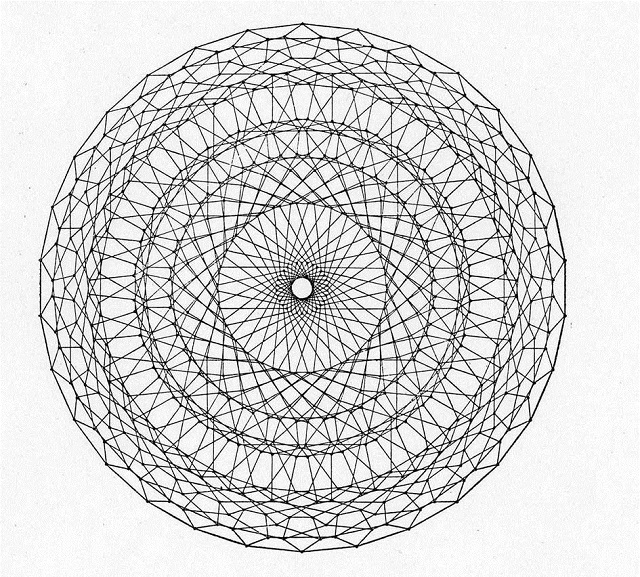
に円の周りの６４本の釘を均等に打ち，３１飛びから始まり，２９飛び，２３，１９，１７，１３，１１飛びに色付き糸をかけて作った「素数曼陀羅」（山見はるか作）という作品が紹介されている．

　高次元多胞体の投影図のようにも見える面白い作品である．ただし，最後は素数ではなく９飛びになっているそうである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　［参］岡本健太郎「アートで魅せる数学の世界」技術評論社

には円の周りの100本の釘を均等に打った周期的糸掛け曼荼羅に続き、非整数、らせんやエピサイクロイド・ハイポサイクロイド、リサージュ曲線などのストリングアートが紹介されている。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝