平面らせんには

ベルヌーイらせん(r=aθ,対数らせん)

アルキメデスらせん(r=aθ)

フェルマーらせん(r=a√θ,放物らせん)

ｒ=a/θ(双曲らせん)

ｒ=a/√θ (ラッパ線)

ｒ=aθ2, r=aθk (代数らせん)

などの種別がある。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

葉序則 (phyllotaxis)について考えてみたい。

黄金角とは360°を1:τに内分した角度(137.5 / 222.5°)であるが、葉序則は偏角θの規則性であって，動径rの規則ではない

これらを平面上にプロットするには

x=r(θ)cosθ

y=r(θ)sinθ

とするのであるが、アルキメデスらせん上の点配置 (r=aθ)とすべきか、アルキメデスらせんとフェルマーらせんの中間的ならせん上の点配置 (r1.5=aθ)とすべきか

フェルマーらせん上の点配置 (r2=aθ)とすべきかは葉序則とは無関係なのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

試しにアルキメデスらせん上にα=137.5°で点配置すると中心部に集中することが見て取れるだろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
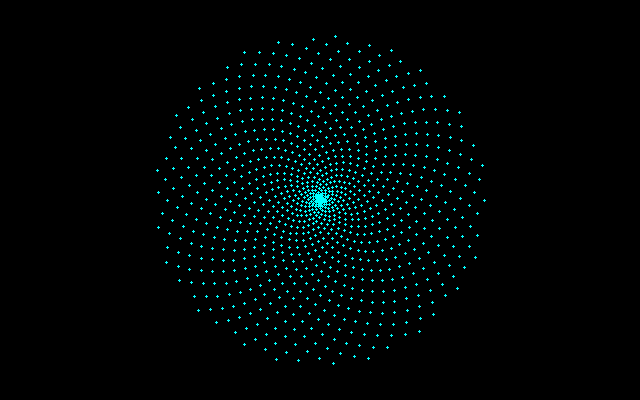
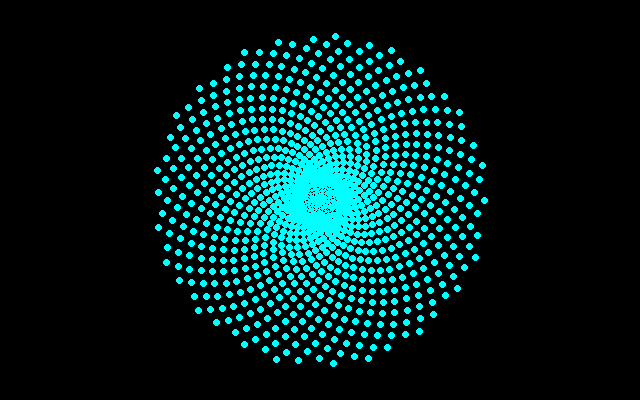