［２］回転する正三角形の追跡問題

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

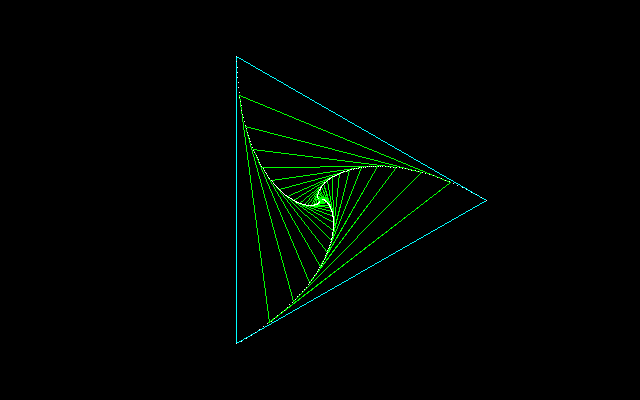
1辺の長さが1の正三角形を考える。3頂点が辺上を時計回りにaだけ移動すると、元の正三角形に内接する少し小さな正三角形ができる。

その辺長は

x={a^2+((1-a)^2-2a(1-a)cos60}^1/2=(3a^2-3a+1)^1/2

となる。

この操作を無限に続けていくと、渦巻は正三角形の中心でぶつかり、1本の渦の長さは

L=a+ax+ax^2+ax^3+・・・=a/(1-x)=a/{1-(3a^2-3a+1)^1/2}

={1+(3a^2-3a+1)^1/2}/3(1-a)

となる。

a→0のとき、L→2/3となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正三角形の頂点と重心間の距離をbとすると

bcos30=1/2→b=1/√3

b^2+b^2tan^2(30)=b^2/cos^2(30)＝4/9

√(4/9)=2/3=L

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝