仭惓懡柺懱杺曽恮乮偦偺俀俀乯
[Q]愗椗棫曽懱偺捀揰偱傕偱偒傞偱偟傚偆偐丠
捀揰悢32
曈悢48
柺悢18乮榋妏宍柺12丄惓曽宍柺6乯
侾捀揰偵夛偡傞柺偼俁柺偱丄榋妏宍俁柺偺捀揰偑俉屄丄惓曽宍丒榋妏宍丒榋妏宍偺捀揰偑俀係屄偱偡丅
榋妏宍俁柺偺捀揰偵偼侾乣俉偺悢帤傪怳傟偽偄偄偐側偲巚偄傑偟偨丅 乮嶳丂寷媣乯
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
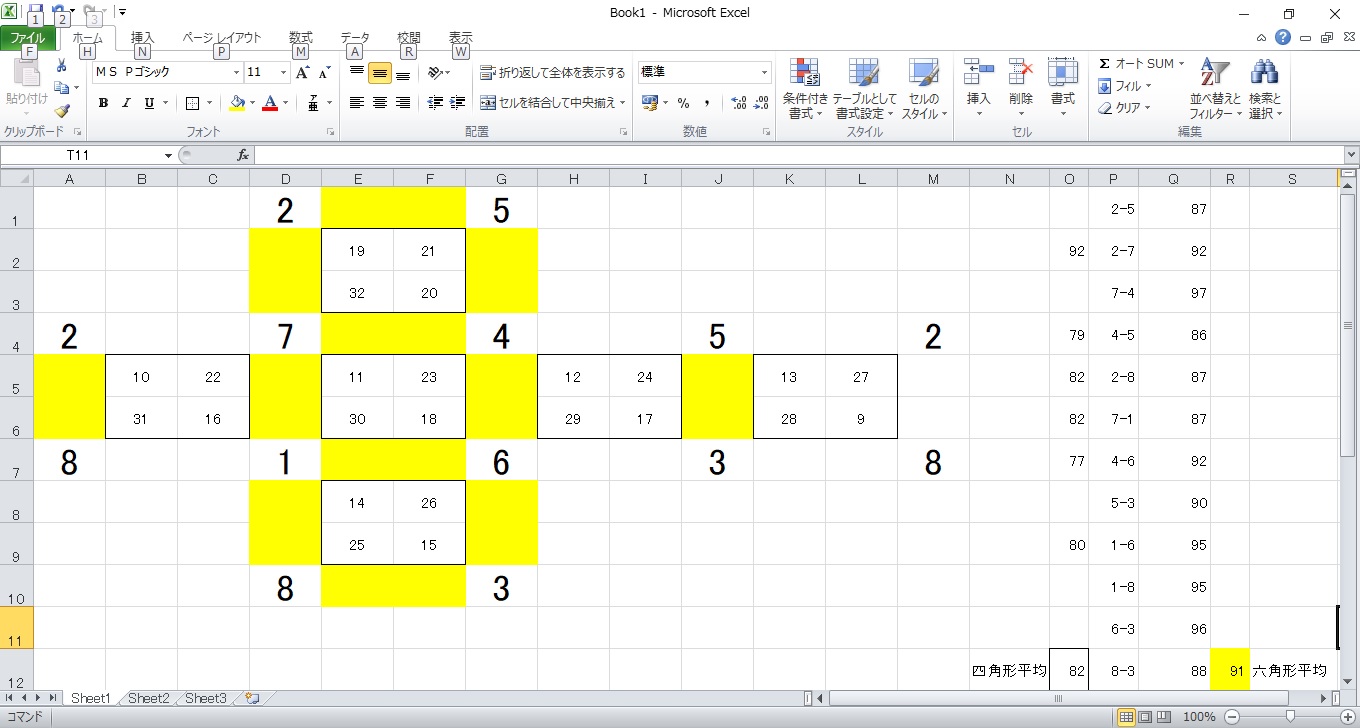
愗椗棫曽懱偱揔摉偵帋偟偰傒傑偟偨偑丄榋妏宍柺崌寁偼巐妏宍柺崌寁傛傝傕暯嬒偟偰俋傎偳戝偒偔側傞傛偆偱偡丅偙偺偙偲傪愢柧偡傞曽朄偑偁傞偺偱偼側偄偱偟傚偆偐丠傕偟偁傟偽俀庬椶埲忋偺柺偑偁傞懡柺懱偼彍奜偱偒傑偡偹丅 乮嶳丂寷媣乯
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
1+2+3+丒丒丒+8=36
奺捀揰偼3夞偢偮廳暋偟偰悢偊傜傟傞偐傜丄榋妏柺偺廃傝偺榓偼36丒3/12亖9
僴儈儖僩儞宱楬傪
1仺2仺3仺4仺5仺6仺7仺8仺1
偲偮側偖偲丄柺廃埻偺榓傪3,5,5,7,9,9,9,9,11,13,13,15偵偡傞偙偲偑偱偒傞丅
惓曽宍柺偺廃傝偺榓傪x,榋妏宍柺偺廃傝偺4捀揰偺榓傪x-3,x-5,x-5,x-7,x-9,x-9,x-9,x-9,x-11,x-13,x-13,x-15
榓偼12x-108
1+2+3+丒丒丒+24=25丒12=300
6x+12x-108=900
18x=1008,x=56
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
24屄偺捀揰偵9乣32傑偱偺悢抣傪攝抲偡傞偲偟偰丄惓曽宍柺偺廃傝偵偼56+32=88偵側傞傛偆偵攝抲偡傟偽傛偄偙偲偵側傞

亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖




