■正12面体と正20面体の発見(その9)
「4次元正多胞体は6個より多くは存在しない」ことを証明してみよう。
少なくとも3つの胞が1つの辺に集まらなければならない。
1つの辺に集まる二面角の総計は360°より小さくならなければならないからだ。
===================================
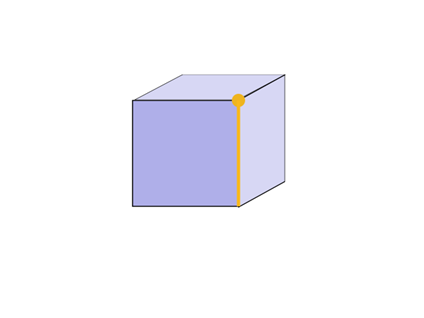
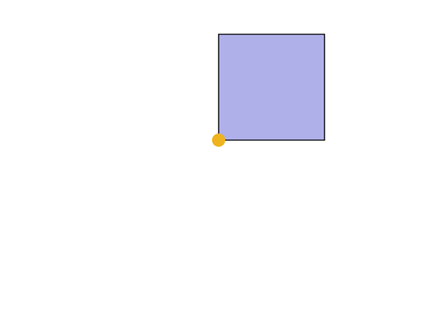
立方体の二面角はcosδ= 0、90°である
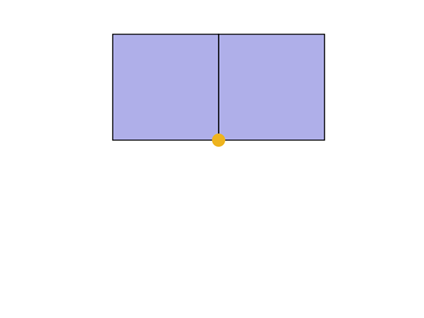
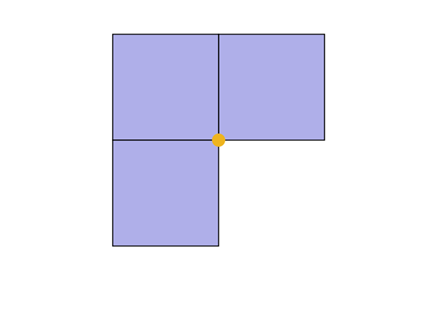
3個の立方体をを一つの辺に集めることはできるが、4個はできない
===================================
こうして正八胞体の存在が説明される
===================================







