■追跡曲線(その32)
n匹のイヌが正n角形の頂点に1匹ずついたとして,それぞれ同じ速さで隣りのイヌを追いかけるとする.この場合も,イヌのたどる軌跡は等角らせんになる.
n=4の追跡曲線は
[参]ウェルズ「不思議おもしろ幾何学事典」朝倉書店
の表紙デザインにもなっている.
等角らせんの一部を拡大あるいは縮小したとしても,もとの等角らせんの別の部分と重なるから,等角らせんは自己相似である.したがって,
r=aexp(−bθ)
すなわち,中心角θが一致の角度進む毎に中心からの距離rの値が一定倍になる回転する正n角形の頂点の軌跡を描けば,追跡曲線の等角らせんとなる渦巻き
(x,y)=(rcosθ,rsinθ)
を描くことができる.
以下に,渦巻き図を掲げるが,θが1進む毎にrの値はexp(−b)倍になるから,停止則は,exp(−bθ)<0,01になったときに設定してある.
===================================
[1]回転する正三角形の追跡問題
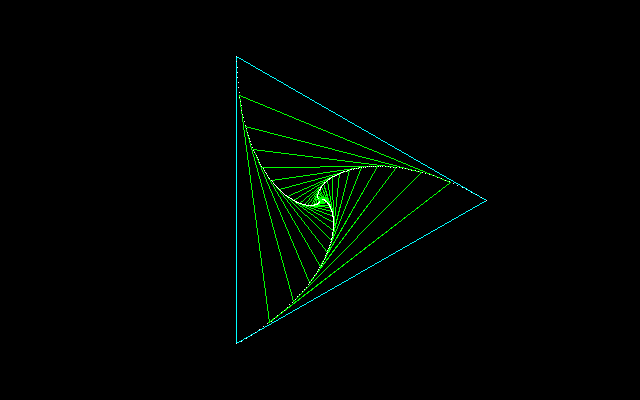
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[2]回転する正方形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[3]回転する正五角形の追跡問題

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[4]回転する正六角形の追跡問題

===================================






