以下の図のような骨組みをスケルトンと呼ぶことにする。

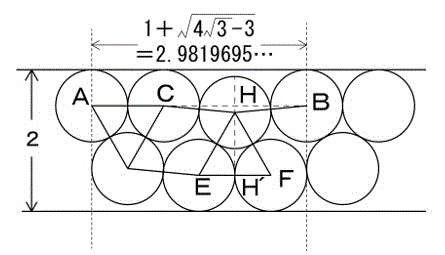
ここでは

　　[参]フランクル・前原「幾何学の散歩道」共立出版

にあるもうひとつのスケルトンで周期を算出して、個数を計算してみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

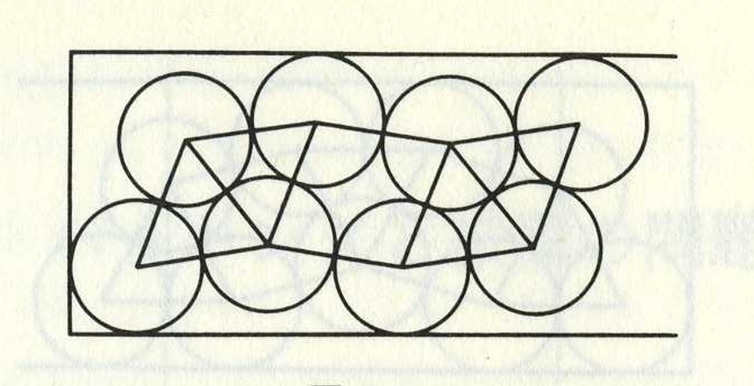
　計算の都合上単位円とする。円１の中心は(1,1)

円4の中心と円1の中心の中心間距離は2√3

縦方向の距離は2であるから

横方向の距離は2√2

円4の中心は(1+2√2,3)

中点は(1+√2,2)、傾きは1/√2となる。

円2、円3の中心を(x,y)とすると

(x-1)^2+(y-1)^2=4

y-2=-√2(x-1-√2)=-√2(x-1)+2

y-1=-√2(x-1-√2)=-√2(x-1)+3

3(x-1)^2-6√2(x-1)+5=0

X-1= （3√2±√3）/3＝√2±1/√3

(y-1)^2=4-(x-1)^2＝4-2±√(8/3)-1/3＝5/3±√(8/3)

y-1=(√3±√2)/3

これより

円2の中心は(1+√2-1/√3,1+（√3+√2)/3 ）

円3の中心は(1+√2+1/√3,1+（√3-√2)/3）

円5の中心と円3の中心の中心間距離は2

縦方向の距離は（√3-√2)/3であるから

横方向の距離は4-(5-2√6）/3=(7+2√6)/3の平方根（√6+1)/√3

円5の中心は(1+2√2+2/√3,1）

円7の中心は(1+3√2+3/√3,1（√3-√2)/3）

周期は円1と円5を比較すると

2√2+2/√3

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝