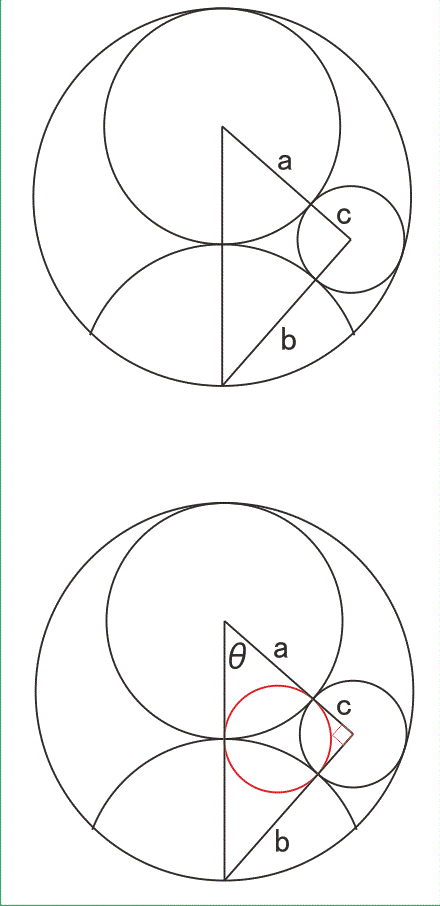
大円（半径ａ），扇（半径ｂ），小円（半径ｃ）が下図のような位置にある（外側の円の半径を１とする，２ａ＋ｂ＝２）．それらの中心を結ぶ三角形は直角三角形である．（この問題では，ｃ円が外円に接することは要求されていないことに注意．）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ］ｂ扇とｃ円の間の接線が直角三角形の内接円の中心を通ることを示せ．

　ｃ円の中心を（ｘc，ｙc）とすると

　　Ｓ＝１／２・（ｂ＋ｃ）（ｃ＋ａ）＝１／２・ｘc（ａ＋ｂ）

　　ｘc＝（ｂ＋ｃ）（ｃ＋ａ）／（ａ＋ｂ）

　　ｙc＝（ｂ＋ｃ）ｓｉｎθ−１＝（ｂ＋ｃ）^2／（ａ＋ｂ）−１

　接点を（ｘ0，ｙ0）とすると，相似比ｂ／（ｂ＋ｃ）より，

　　ｘ0＝ｘc・ｂ／（ｂ＋ｃ）＝ｂ（ｃ＋ａ）／（ａ＋ｂ）

　　ｙ0＝（ｙc＋１）・ｂ／（ｂ＋ｃ）−１＝ｂ（ｂ＋ｃ）／（ａ＋ｂ）−１

　ｂ扇：ｘ^2＋（ｙ＋１）^2＝ｂ^2上の接点（ｘ0，ｙ0）における接線は

　　ｘ0ｘ＋（ｙ0＋１）（ｙ＋１）＝ｂ^2

　直角三角形の内心は（ｃ，ｂ−１），接線が内心を通るならば

　　ｘ0ｃ＋（ｙ0＋１）ｂ＝ｂ^2

　　ｂｃ（ｃ＋ａ）／（ａ＋ｂ）＋ｂ^2（ｂ＋ｃ）／（ａ＋ｂ）＝ｂ^2

　　ｂｃ（ｃ＋ａ）＋ｂ^2（ｂ＋ｃ）＝ｂ^2（ａ＋ｂ）

　　ｃ（ｃ＋ａ）＋ｂ（ｂ＋ｃ）＝ｂ（ａ＋ｂ）

　　ｃ（ｃ＋ａ）＝ｂ（ａ−ｃ）

　　ｃ^2＋ｃａ＝ａｂ−ｂｃ

　　ａｂ＝ｃ（ａ＋ｂ＋ｃ）

が成り立つことになるが，これは前問より保証されている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ］ｂ扇とｃ円の間の接線が外側の円の中心を通るとき，ａの値を求めよ．

［Ａ］接線：ｘ0ｘ＋（ｙ0＋１）（ｙ＋１）＝ｂ^2が（０，０）を通るためには

　　（ｙ0＋１）＝ｂ^2

　　ｂ（ｂ＋ｃ）／（ａ＋ｂ）＝ｂ^2

　　ｂ（ｂ＋ｃ）＝ｂ^2（ａ＋ｂ）

　　（ｂ＋ｃ）＝ｂ（ａ＋ｂ）

が成り立つことが必要である．

　　ｃ＝ａｂ＋ｂ^2−ｂ＝ｂ（ａ＋ｂ−１）＝（２−２ａ）（１−ａ）＝２（１−ａ）^2

　　ｃ＝［−（２−ａ）＋｛４＋４ａ−７ａ^2｝^1/2］／２

と比較すると

｛４＋４ａ−７ａ^2｝^1/2＝４（１−ａ）^2＋（２−ａ）＝４ａ^2−９ａ＋６

４＋４ａ−７ａ^2＝１６ａ^4＋８１ａ^2＋３６−７２ａ^3−１０８ａ＋４８ａ^2

＝１６ａ^4−７２ａ^3＋１２９ａ^2−１０８ａ＋３６

１６ａ^4−７２ａ^3＋１３６ａ^2−１１２ａ＋３２＝０

２ａ^4−９ａ^3＋１７ａ^2−１４ａ＋４＝０

　厳密解はともかく，数値解はａ＝０．６２３９１４となった．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝