さらに問題を改編．

　大円（半径ａ），扇（半径ｂ），小円（半径ｃ）が下図のような位置にある（外側の円の半径を１とする，２ａ＋ｂ＝２）．それらの中心を結ぶ三角形は直角三角形である．（ｃ円の中心はａ円の中心とｂ扇の要を端点とする半円上にある．この場合，内接円の半径ｒはｃ円と同径になることは明らかである．）

　ただし，この問題では，ｃ円はａ円，ｂ扇に接するものの，外円に接することは要求されていないことに注意．

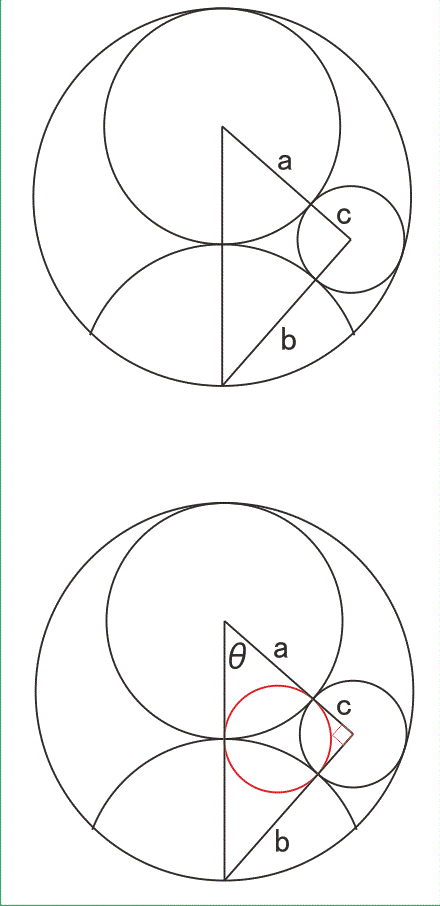
ｃｏｓθ＝（ｃ＋ａ）／（ａ＋ｂ）

ｓｉｎθ＝（ｂ＋ｃ）／（ａ＋ｂ）

ｔａｎθ＝（ｂ＋ｃ）／（ｃ＋ａ）

ｔａｎθ／２＝ｓｉｎθ／（１＋ｃｏｓθ）＝（ｂ＋ｃ）／（２ａ＋ｂ＋ｃ）

ｔａｎθ／２＝（１−ｃｏｓθ）／ｓｉｎθ＝（ｂ−ｃ）／（ｂ＋ｃ）

が成り立つ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　中心を結ぶ三角形が直角三角形であるとき，内接円の半径ｒはｃ円と同径になることは明らかであるが，ａ円，ｂ扇との関係も求めておきたい．

　ピタゴラスの定理より

　　（ａ＋ｂ）^2＝（ｂ＋ｃ）^2＋（ｃ＋ａ）^2

整理すると

　　ａｂ＝ｃ（ａ＋ｂ＋ｃ）

　一方，直角三角形の面積Ｓは

　　Ｓ＝１／２・（ｂ＋ｃ）（ｃ＋ａ）

また，（直角三角形でなくても）

　　Ｓ＝１／２・ｒ（２ａ＋２ｂ＋２ｃ）＝ｒ（ａ＋ｂ＋ｃ）

が成り立つから

　 ２ｒ（ａ＋ｂ＋ｃ）＝（ｂ＋ｃ）（ｃ＋ａ）＝ｂｃ＋ｂａ＋ｃ^2＋ｃａ

　ａｂ＝ｃ（ａ＋ｂ＋ｃ）を代入すると

　 ２ｒ（ａ＋ｂ＋ｃ）＝２ｃ（ａ＋ｂ＋ｃ）→ｒ＝ｃ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ］中心を結ぶ三角形が直角三角形であるとき，ａの取り得る範囲を求めよ．

［Ａ］前節より

　　ａｂ＝ｃ（ａ＋ｂ＋ｃ）

　　ｃ^2＋（ａ＋ｂ）−ａｂ＝０

　　ｃ＝［−（ａ＋ｂ）＋｛（ａ＋ｂ）^2＋４ａｂ｝^1/2］／２

ｃをａで表すために，ｂ＝２−２ａを代入すると

　　ｃ＝［−（２−ａ）＋｛（２−ａ）^2＋８ａ（１−ａ）｝^1/2］／２

　　ｃ＝［−（２−ａ）＋｛４＋４ａ−７ａ^2｝^1/2］／２

　４＋４ａ−７ａ^2≧０より

ａ≧（−２±√３０）／７＝０．４９６７５・・・

　｛４＋４ａ−７ａ^2｝≧（２−ａ）^2はａ≦１と同値であるから，

　（−２±√３０）／７≦ａ≦１

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝