大円（半径ａ），扇（半径ｂ），小円（半径ｃ）が下図のような位置にある（外円の半径を１としても一般性は失われない，２ａ＋ｂ＝２）．

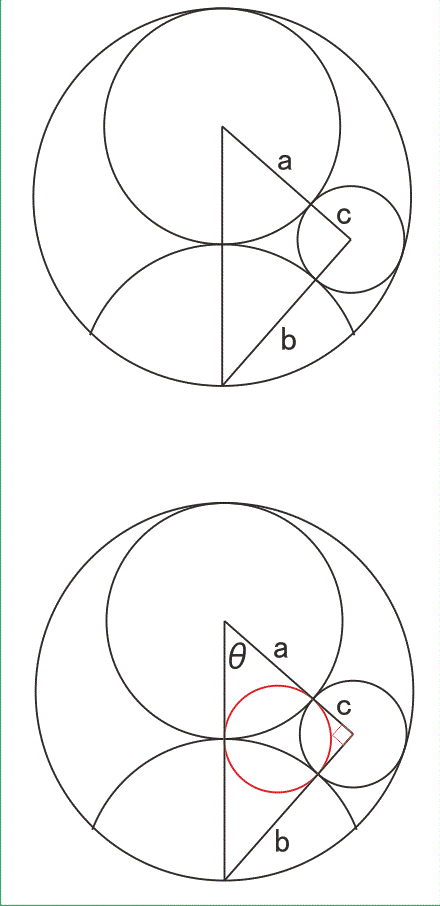
　（その４）は元々「算額の問題」で，それらの中心を結ぶ三角形が直角三角形である場合に改編した問題を掲げたい．

［Ｑ］それらの中心を結ぶ三角形が直角三角形であるときのａの値を求めよ．（ｃ円の中心はａ円の中心とｂ扇の要を端点とする半円上にある．）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ａ］ピタゴラスの定理より

　　（ａ＋ｂ）^2＝（ｂ＋ｃ）^2＋（ｃ＋ａ）^2

整理すると

　　ａｂ＝ｃ（ａ＋ｂ＋ｃ）

　　ｃ^2＋（ａ＋ｂ）−ａｂ＝０

　　ｃ＝［−（ａ＋ｂ）＋｛（ａ＋ｂ）^2＋４ａｂ｝^1/2］／２

ｃをａで表すために，ｂ＝２−２ａを代入すると

　　ｃ＝［−（２−ａ）＋｛（２−ａ）^2＋８ａ（１−ａ）｝^1/2］／２

　　ｃ＝［−（２−ａ）＋｛４＋４ａ−７ａ^2｝^1/2］／２

　（その４）より

　　ｃ＝（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）

　したがって，

［−（２−ａ）＋｛４＋４ａ−７ａ^2｝^1/2］／２＝（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）

［−（２−ａ）＋｛４＋４ａ−７ａ^2｝^1/2］＝２（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）

｛４＋４ａ−７ａ^2｝^1/2＝２（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）＋（２−ａ）

｛４＋４ａ−７ａ^2｝^1/2＝（ａ^3−２ａ^2−２ａ＋４）／（ａ^2−２ａ＋２）

を解くことになるが，あとは読者の宿題としたい．なお，内接円の半径ｒはｃ円と同径になることは明らかである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝