番外編として，中川宏さんに教えてもらった問題を掲げたい．大円（半径ａ），扇（半径ｂ），小円（半径ｃ）が下図のような位置にある（外円の半径を１としても一般性は失われない，２ａ＋ｂ＝２）．

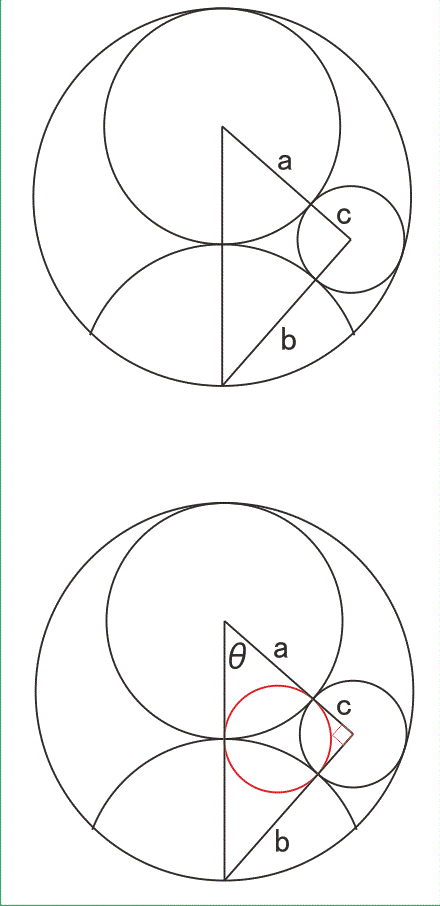
［Ｑ］ａを動かしたとき，ｃの最大値を求めよ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ａ］ｃ円の中心を（ｘ，ｙ）とする．

［１］ａ円の中心（０，１−ａ）からの距離に関して

　　ｘ^2＋（ｙ−１＋ａ）^2＝（ａ＋ｃ）^2

［２］ｂ扇の要（０，−１）からの距離に関して

　　ｘ^2＋（ｙ＋１）^2＝（ｂ＋ｃ）^2

［３］外円の中心（０，０）からの距離に関して

　　ｘ^2＋ｙ^2＝（１−ｃ）^2

　（ｘ，ｙ）を消去する．

［２］ｘ^2＋ｙ^2＋２ｙ＋１＝（ｂ＋ｃ）^2

［１］を代入すると

２ｙ＝（ｂ＋ｃ）^2−（１−ｃ）^2−１・・・［４］

［３］ｘ^2＋ｙ^2−２（１−ａ）ｙ＋（１−ａ）^2＝（ａ＋ｃ）^2

［１］を代入すると

２（１−ａ）ｙ＝−（ａ＋ｃ）^2＋（１−ｃ）^2＋（１−ａ）^2・・・［５］

［４］［５］からｙを消去して整理すると

（１−ａ）｛（ｂ＋ｃ）^2−（１−ｃ）^2−１｝＝−（ａ＋ｃ）^2＋（１−ｃ）^2＋（１−ａ）^2

　ｂ＝２−２ａを代入して，ｃについて整理すると

　　ｃ＝（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）

　ｃをａで微分して，ｃ’＝０より，

　　ａ^4−４ａ^3＋１０ａ^2−１２ａ＋４＝０

　解がａ＝１に関して対称となるようなので，

　　ａ^4−４ａ^3＋６ａ^2−４ａ＋１＋４ａ^2−８ａ＋４−１＝０

　　（ａ−１）^4＋４（ａ−１）^2−１＝０

　　±（ａ−１）^2＝−２±√５

　　（ａ−１）^2＝−２＋√５，（ａ−１）^2＝２＋√５

　　（ａ^2−２ａ＋３−√５）（ａ^2−２ａ−１−√５）＝０

　　ａ＝１±（−２＋√５）^1/2，１±（２＋√５）^1/2

　題意を満たすものは，ａ＝１−（−２＋√５）^1/2

　　ａ^2−２ａ＝√５−３，ａ^2−２ａ＋２＝√５−１

　（ａ^3−３ａ^2＋２ａ）＝ａ（ａ−１）（ａ−２）

＝（ａ^2−２ａ）（ａ−１）

＝（３−√５）（−２＋√５）^1/2

　　ｃ＝（ａ^3−３ａ^2＋２ａ）／（ａ^2−２ａ＋２）

＝（√５−１）／２・（−２＋√５）^1/2／４

＝｛（−１１＋５√５）／２｝^1/2

　「一関算額の問題」と同様，因数分解に苦戦したが，何とか解くことができたようだ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝