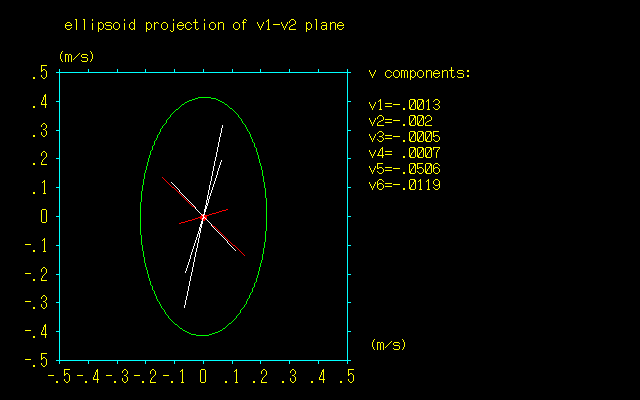
ロボットアームと６次元楕円体（その１）

　「閑話休題」を書き始めてから，これまでにアップロードしたコラム数は１３０話を超えた．ネット検索のアクセスカウントもアップしているようであるし，結構いろいろなところで利用されているらしい．なかには，書いた本人が思いも寄らないような使われ方がされている場合もあり，昨年，東大の秦浩司先生（現・ハザマ技術研究所）の研究課題の誤差を評価するために考えだされた「ｎ次元楕円を投影する方法」がいまひょんな所で役に立っている．

　秋田大学・工学資源学研究科・ロボティクス・福祉工学講座の佐々木誠先生（makoto@control.mech.akita-u.ac.jp）から伺った話によると，ロボット工学の分野においてはアームの設計，マニピュレータの制御問題，障害物回避問題などがひとつの重要な研究対象になっているのだが，ロボットアームの機能を評価したり，動作を最適に制御するためにはｘ方向・ｙ方向・ｚ方向の速度，ｘ軸まわり・ｙ軸まわり・ｚ軸まわりの角速度を同時にコントロールしなければならない．

　これを「６軸制御」というのだそうだが，その際，６次元楕円が必要になり，コラムに掲げた方法が有用とのことであった．いろいろな使い道があるものだと感心したが，予期せぬ効用の好例といえるだろう．

　超楕円体についてネット検索していたところ，『ｎ次元楕円の陰と影』というコラムに行き着きました．実は，現在６次元楕円を描写したいと考えております．Ａ（６×６）の行列をＵΣＶ’に特異値分解すると，Ｕの要素を主軸方向，Σの要素つまり特異値が半径とする楕円体が描写できるはずです（中略）．

　なぜ６次元楕円体が必要か？　ロボット工学の分野には，ロボットアームの評価法として，可操作性楕円体という概念があります．内容は，qを関節角速度とすると，ユークリッドノルム∥q∥＝(q1^2+q2^2+・・・+q6^2)^(1/2)が１以下を満足するようなアーム（７関節）の関節角速度を用いて実現しうる手先速度ｖの集合がｍ次元ユークリッドノルム空間内になり，３次元空間における手先の位置と姿勢を考えるとｍ＝６となります．大抵は，アームの関節を減らし，３次元ユークリッドノルム空間にして考えられています．

　また，ｖ＝Ｊｑという関係式も成り立ち，Ｊは６×７のヤコビ行列を表します．ヤコビアンに関しては，２次元で扱う場合，手先位置座標を関節角度変数で１階微分したものとなります．３次元（作業空間）で扱う場合，つまり今回の場合は，関節回転軸×（関節点から手先位置への位置ベクトル）および関節回転軸で構成されます．さらに，楕円体はｖ’Ｊ~’Ｊ~ｖが１以下，かつ，ｖはＪの値域に含まれます（’は転置を示す）・・・というようなものです．

　ここで，今回の６次元楕円体とは手先の並進と回転の速度ｖを示します．ｖ1～ｖ3までは速度（単位m/s），ｖ4～ｖ6までは角速度（rad/s）となります．よって２次元平面の切り口でみたいというのは，手先の発生しうる速度が手先位置によってどのように変化するか？　ある位置で，ｘｙｚ方向にどの程度の速度を出せるか？　というものを表したいのです．

　ロボット工学ではこれまで６次元楕円体の描写に関する議論がなされていないこと，それによってロボットアームの手先の自由度が６となるような運動が評価できていなかったのですが，ｖ＝ＪｑのＪがいまわかっているので，Ｊを特異値分解してみるという流れで行ってみました．ところが，実際問題，６次元という大きな壁にぶつかり，ご相談している次第であります．ご助言いただければ幸いであります．

　次元というのは，独立なパラメータの個数と考えられるので，問題が何次元になろうが驚く必要はありません．

　ところで，参考文献：吉川恒夫先生のロボット制御基礎論（コロナ社）によると，いま問題にしているのは「可操作性楕円体」といい，長軸ほど早い速度で動ける方向を表しているとのことでした．

　もうひとつ「操作力楕円体」というものがあり，その関係式はτ＝Ｊ~ｆで，ｆは力とモーメントの要素，τは関節に働くトルクを示します．操作力楕円体はｆ’Ｊ~’Ｊ~ｆ≦１の楕円体となり，一般に可操作性楕円体と直交するような楕円体になることが知られています．

　どちらも数学的な構造は同じものですから，可操作性楕円体，すなわち，ｖ＝Ｊｑ（ｑ＝Ｊ~ｖ）のとき，超楕円体

　また，メールには「２次元平面の切り口でみたい」とありますが，どうやらそれは「２次元平面への正射影をみたい」の誤解のようでした．正射影と切り口にそれぞれ統計学上の用語を対応させると，正射影は「相関」に相当するものですが，切り口は「偏相関」すなわち，他の変数の影響を除いた相関の強さを意味しています．それに対して，通常の相関はみかけ上の相関を含んだ全相関を意味しています．

　ともあれ，３次元世界で人の顔を映すならば三面鏡で十分なのですが，６次元世界に住む人間では１５面鏡（v1-v2,v1-v3,v2-v3などそれぞれのv1～v6の各組み合わせの２次元平面への正射影）を用いなければ全体像を映し出すことはできません．

　また，ｖ1～ｖ3は速度，ｖ4～ｖ6は角速度とありますから，ロボットアームの場合，３次元速度空間（ｖ1，ｖ2，ｖ3）あるいは角速度空間（ｖ4，ｖ5，ｖ6）への正射影，さらには３次元空間での切り口を求めることも必要になるものと思われました．

　さて，６次元楕円であっても，楕円の赤道面の(vi,vj)平面への正射影を描くことは，単なる座標変換で済みますから，簡単に解決できる問題です．その際の座標変換式は，以下の手順で求めることができます．

　ただし，文献にある解説では２次元楕円を２次元平面に描く場合であっても，かなり面倒な方法を使って楕円を求めています．数学的にいえば，簡単なユニタリ変換で済むところをわざわざ難しくしているという感さえあります．そのため，文献の方法はお勧めしませんし，とても６次元楕円の正射影を求められそうにもありません．

　次に，楕円の(vi,vj)平面での切り口の形を描くためには，vi,vj成分以外はすべて０ですから，ヘシアンの固有値・固有ベクトルを求めずとも標準形に直すことができ，簡単に切り口の形を計算できます．

　ここで，Ｈijとは，行列Ｈに対して添字ｉ，ｊで指定した行・列を取り出して得られる小行列という意味であって，ｉ行とｊ列を取り除いたものでないことに注意して下さい．

　それに対して，６次元楕円の(vi,vj)平面への正射影の形を求めることはそれほど易しい問題ではありません．

　われわれが３次元空間内の曲面をみるときは，ちょうど写真を撮るように２次元の面に射影していると考えられます．山を眺めると稜線がみえます．それは接平面が視点を通るような曲面上の点の軌跡を視平面に射影した輪郭なのです．６次元楕円でも本質的な考え方は同じなのですが，法線方向が１つではないので，高次元空間に馴れていないわれわれにとっては計算が複雑になり，簡単にはいかないのです．

　しかし，輪郭を求める考え方自体は切り口の求め方によく似ていて，いわば局所的な固有値（？）を２次方程式を解くことによって求めるだけで正射影の計算ができるのです．詳細についてはコラム『ｎ次元楕円の陰と影』をご覧頂きたいのですが，ここで，正射影を求めるプロシージャをまとめておきます．

　すなわち，正射影を求めるにはヘシアンの固有値・固有ベクトルの計算は不要ですが，逆行列の計算が不可避と考えられました．また，長軸，短軸を固有値の大きさを用いて定めることによって描くことができるのですが，切り口が軸の長さを√λで割ってやるのに対して，正射影では√λを掛けなければなりません．

　以上により，切り口を求めることと正射影を求めることは「表と裏の関係」にあることが理解されます．

　６次元楕円の極や赤道はヘシアンから直接的に固有値と固有ベクトルを計算することによって得られますし，その方が一般的でしょう．しかし，逆行列の固有値は元の行列の逆数となりますし，また，固有ベクトルは変わりませんから，ヘシアンの逆行列を用いても赤道面の正射影を描くことができます．ただし，その手順は長くなってしまいます．

の手順で描くことができます．これまでの議論からこの方が正攻法の描き方であることがおわかり頂けるでしょう．しかし，正射影を描く場合，

とすると手順を１回省くことができるという利点があり，また，切り口と「表と裏の関係」にあることがわかりやすくなるのです．

　固有値を求め，標準形にするところは簡単にわかると思われますが，それではなぜ正射影の場合，逆行列をとる必要があるのでしょうか？

　輪郭の計算は，接平面（法線ベクトル）を求めるという微分幾何学の基本的な知識と線形代数学の方法（ヤコビの公式，シルベスターの定理など）によって説明できるのですが，長くなりますし，証明に興味をお持ちの方も少ないでしょうから，ここではその証明を割愛します．

　統計学的にみると，これは「誤差伝播の法則」に基づいているのですが，統計の世界では昔から使われている考え方であって，次のように説明されます．

　上記のヘシアンは，フィッシャーの情報行列（Fisher's information matrix）と呼ばれるものに対応していて，この行列の逆行列は，いわゆる分散共分散行列であって，その対角要素はパラメータの精度を与える重要な性質をもっています．

と表されるのですが，分散共分散行列はすべてのパラメータが独立と考えられる場合は対角行列，また，パラメータ間に強い相関がある場合には非対角要素は無視できなくなり対称行列となります．

　すなわちｖi方向の拡がりを決定するものが，分散共分散行列なのですが，これによって，たとえば，ｖ1方向の拡がりは主としてｖ1の誤差に基づくのですが，他の要素ｖ2～ｖ6の誤差の影響も受ける形に変換されるのです．参考文献として吉沢康和「新しい誤差論」共立出版を掲げておきます．

　以下に，６次元楕円の正射影を２次元平面に投影するプログラムを掲げます．このプログラムを実行すると，２次元平面vi-vjへの正射影１５画面分の楕円が１枚ずつ次々に表示されますが，１５枚まとめて画面に描写するようにした方がいいかもしれません．

3720 IF S3=0 THEN CCC=PI/2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ELSE B3=(S2-S1+SQR((S1-S2)*(S1-S2)+4*S3*S3))/2/S3:CCC=ATN(B3)

　しかし，この方法では軸の対応がずれてしまうことが起こり得ます．そのため，3840行～3920行では，２次方程式を解く代わりに，回転行列

　一方，切り口を求める場合は，ヘシアンそのものを用いて同じ計算をしますが，正射影では，＊行で軸の長さに√λを掛けているのに対して，切り口では軸の長さを√λで割らなければなりません（4450～4460行）．

　６次元楕円では実対称行列を扱いますから，固有値はヤコビ法で計算しています．ヤコビ法はすべての固有値・固有ベクトルが同時に求められる，最も実用に適した優れた計算法です．ほかにもいろいろな方法がありますが，理論が難解なもの，計算手順が複雑なもの，プログラム作成が難しいもの，計算時間がかかるもの，収束が確実ではないもの，などが多いのです．

　固有値は大きい順に並べ替えて使われることが多いのですが，それでは座標軸との関係が一致しなくなりますから，ロボットアームの問題では軸との対応関係が保たれなければなりません．そこで気がかりなのは固有値計算における対応関係の保持です．

　固有値問題の性質として，逆行列の固有値は元の行列の逆数となり，また，固有ベクトルは変わりません．しかし，ここに掲げたプログラムでは，直接ヘシアンから固有値・固有ベクトルを求めた場合（λ1，・・・，λ6）とヘシアンの逆行列経由で固有値・固有ベクトルを求めた場合（δ1，・・・，δ6）とで，その対応関係がくずれてしまう（δi≠１／λi）という困った現象が見つかっています．

　そのため，計算上の対策を施さなければいけないということがわかりました．もしＲ’ＶＲが対角行列ではなく，上半角行列でいいのであれば，ＱＲ法，ＬＵ分解などの行列分解のスキームが適用できます．そこで，まず最初にＬＵ法やＱＲ法を用いて固有値を計算する手も考えたのですが，固有値だけでなく，固有ベクトルも欲しいので，ＱＲ法，ＬＵ分解はＮＧ．それよりは６次元楕円の正射影と極を同時に描くことによって，軸との対応関係の不整をチェックする方法をとることにしました．

　正射影を求めるサブルーチンは3830～4010行なのですが，いわば局所的な条件のみに基づいて，回転行列を用いて楕円半径と楕円の配向を定めていますから，６次元楕円の固有値・固有ベクトルには依存しません．

　それに対して，極や赤道面は固有値・固有ベクトルに依存するのですが，正射影は局所的な条件によって定まるので，整合の良し悪しはある程度この方法で確認することが可能になります．とはいっても，完全とはいえないのですが，正しく描かれると，２次元平面への正射影のなかにすべての極や赤道面が含まれることになります．