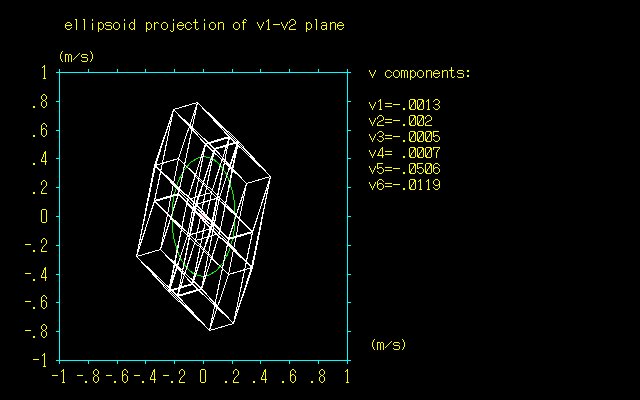
■ロボットアームとn次元直方体(その2)
0次元の点がまっすぐ動くと1次元の線分になる.1次元の線分が平面の上で自分と直角の方向に同じ長さだけ動くと,2次元の正方形になる.2次元の正方形が3次元空間の中で自分と直角方向に1辺の長さだけ動くと,3次元の立方体となる.この3次元立方体が4次元空間の中で自分と直角方向に1辺の長さだけ動くと,同じ大きさの8個の立方体からなる4次元の立方体(正8胞体)になる・・・.
こうしてn次元立方体ができあがるが,n次元立方体(正2n胞体)を2次元平面上へ正2n角形を外殻とするように直投影することができることは既に(その1)で述べたとおりである.今回のコラムでは,n次元立方体(直方体)を2次元平面上に実際に描くことを試みたい.
===================================
n次元立方体は,
頂点数: 2^n,
稜数: 2^(n-1)n,
四角形数:2^(n-3)n(n−1)
からなっている.このうち,頂点は(±1,±1,・・・,±1)であるから,確かに2^n個あることがわかるだろう.
しかし,実際のプログラミングにあたっては,2^n個ある頂点すべてを作業用配列に積んで記録しておくようなダサイ手は避けたいと思う.その代わり,すべての頂点を重複なく,遺漏なく数え上げるために,2進数を用いることにした.
たとえば,8ビットのデータがあって,それらのON/OFF状態が,
(b7 b6 b5 b4 b3 b2 b1 b0 )
1 0 1 1 0 0 1 0
という状態にあるとしよう.このとき,2進数10110010が,頂点
(+1,−1,+1,+1,−1,−1,+1,−1)
あるいは
(−1,+1,−1,−1,+1,+1,−1,+1)
に対応していると見なすことにすると,すべての頂点を重複も遺漏もなく数え上げることができるのである(4710,4720行).
次に考えるべきことは,n次元立方体の各頂点からはn本の稜がでるということである.頂点
(+1,−1,+1,+1,−1,−1,+1,−1)
の場合,稜の対蹠点の座標は
(−1,−1,+1,+1,−1,−1,+1,−1)
(+1,+1,+1,+1,−1,−1,+1,−1)
(+1,−1,−1,+1,−1,−1,+1,−1)
(+1,−1,+1,−1,−1,−1,+1,−1)
(+1,−1,+1,+1,+1,−1,+1,−1)
(+1,−1,+1,+1,−1,+1,+1,−1)
(+1,−1,+1,+1,−1,−1,−1,−1)
(+1,−1,+1,+1,−1,−1,+1,+1)
となる.
したがって,ビットのON/OFF状態を検査して,bxビットだけを反転(0→1,1→0)できれば,稜を描くことが可能となるだろう.そのためにはビット演算を行うが,たとえば,b6ビットのON/OFF状態を検査するために,2進数
0 1 0 0 0 0 0 0
(すなわち10進数で2^6)と対応するビット毎に論理積演算を行うと,
1 0 1 1 0 0 1 0
× × × × × × × ×
0 1 0 0 0 0 0 0
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 0 0 0 0 0 0 0
のように,上位ビットから下位ビットまですべてのビットが0になる.
もし,b6ビットが1の2進数であれば,
1 1 1 1 0 0 1 0
× × × × × × × ×
0 1 0 0 0 0 0 0
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 1 0 0 0 0 0 0
のように0とはならないから,10進数の2^xとの論理積の関係を利用して,ビットの状態を判定することができるというわけである(4740行,+1→−1,−1→+1の反転は4810行).
このようにして2^n個の頂点からでるすべての稜を求めることができる.ひとつの稜を2回ずつなぞることになるが,それくらいの無駄は許容範囲であろう.以下に,プログラムおよび6次元楕円体とそれに外接する6次元直方体を重ねて描いた図を掲げる.
===================================
1000 '
1010 ' **** robot-arm control ****
1020 ' 2002/01/18 (C) サトウ イクロウ
1030 SCREEN 3,0:CONSOLE ,,0,1
1040 CLS 3:WIDTH 80,25:COLOR 6
1050 GOSUB *INITIALIZE
1060 GOSUB *JACOBIAN
1070 GOSUB *HESSIAN
1080 GOSUB *ELLIPSOID
1180 '
1190 CLS 3
1200 END
1210 '
1220 ' *** 初期設定 ***
1230 '
1240 *INITIALIZE:
1250 RX=.7:RY=.8:BOX=1:KIND=1:POWER=0
1260 IX=.7:IY=.8:MARK=1:CLR=2:DRAW.COLOR=4
1270 TXT.COLOR=6:GRP.COLOR=5:REF.COLOR=6
1280 SCALE.KIND=1:PLOT=1
1290 PI=3.14159
1300 JX=.709:JY=1
1310 RX=IX*JX:RY=IY*JY
1320 '
1330 M=6
1340 N1=7
1350 '
1360 MMAX=10:NMAX=10
1370 DIM V(MMAX)
1380 DIM JACOBI(MMAX,NMAX)
1390 DIM AZ(MMAX,MMAX),BZ(MMAX,MMAX)
1400 DIM HESSE(MMAX,MMAX)
1410 DIM COV(MMAX,MMAX)
1420 DIM VO(MMAX),VL(MMAX)
1430 DIM VD(MMAX),VS(MMAX)
1440 DIM UNIT$(MMAX)
1450 DIM EDGE(MMAX)
1460 DIM S(MMAX),S0(MMAX)
1470 DIM GXS(MMAX),GYS(MMAX)
1480 DIM GXE(MMAX),GYE(MMAX)
1490 DIM GZ(MMAX)
1500 '
1510 FOR I=1 TO 3
1520 'VO(I)=0:VL(I)=.5
1530 VO(I)=0:VL(I)=1
1540 VD(I)=5:VS(I)=1
1550 UNIT$(I)="m/s"
1560 NEXT I
1570 FOR I=4 TO 6
1580 'VO(I)=0:VL(I)=2
1590 VO(I)=0:VL(I)=4
1600 VD(I)=4:VS(I)=1
1610 UNIT$(I)="rad/s"
1620 NEXT I
1630 RETURN
1640 '
1650 ' *** ヤコビアンの読み込み ***
1660 '
1670 *JACOBIAN:
1680 RESTORE *J
1690 FOR J=1 TO M
1700 FOR I=1 TO N1
1710 READ JACOBI(J,I)
1720 NEXT I
1730 NEXT J
1740 '
1750 RESTORE *V
1760 FOR J=1 TO M
1770 READ V(J)
1780 NEXT J
1790 RETURN
1800 '
1810 *J:'[1]
1820 DATA .2084, .0320, .0409,-.0413,-.0032,-.0086, .0033
1830 DATA 0,-.3443, .1829,-.1264,-.0153,-.0227,-.0493
1840 DATA -.3425, .0606,-.1273,-.1929, .0157, .0446,-.0244
1850 DATA 0, .8841, .4161, .1965, .9440,-.3250, .1699
1860 DATA 1, 0, .4550, .8003,-.3106,-.8159, .4470
1870 DATA 0,-.4673, .7873,-.5664,-.1115,-.4782,-.8782
1880 '
1890 *V:'[1]
1900 DATA -.0013
1910 DATA -.0020
1920 DATA -.0005
1930 DATA .0007
1940 DATA -.0506
1950 DATA -.0119
1960 '
1970 '*J:'[20]
1980 DATA .3063,-.1201, .1035, .1037,-.0128,-.0019, .0373
1990 DATA 0,-.1692, .2014,-.2040,-.0076,-.0405,-.0248
2000 DATA -.1289, .1619,-.1761,-.1737, .0217, .0301,-.0311
2010 DATA 0, .8031,-.4195, .3965, .8705, .3581, .0393
2020 DATA 1, 0, .7101, .7037,-.0844,-.5671, .8029
2030 DATA 0, .5958, .5655,-.5896, .4848,-.7418,-.5948
2040 '
2050 '*V:'[20]
2060 DATA -.6581
2070 DATA .0862
2080 DATA .1687
2090 DATA .5254
2100 DATA -1.1528
2110 DATA .7858
2120 '
2130 ' *** ヘシアンと共分散行列 ***
2140 '
2150 *HESSIAN:
2160 FOR M1=1 TO M
2170 FOR M2=M1 TO M
2180 S=0
2190 FOR I=1 TO N1
2200 S=S+JACOBI(M1,I)*JACOBI(M2,I)
2210 NEXT I
2220 AZ(M1,M2)=S:AZ(M2,M1)=S
2230 COV(M1,M2)=S:COV(M2,M1)=S
2240 NEXT M2
2250 NEXT M1
2260 NZ=M
2270 '
2280 GOSUB *INVERSE
2290 '
2300 FOR I=1 TO M
2310 FOR J=1 TO M:HESSE(I,J)=BZ(I,J):NEXT J
2320 NEXT I
2330 RETURN
2340 '
2350 ' ** 逆行列 ( AZ==>BZ ) **
2360 '
2370 *INVERSE:' [GAUSS-JORDAN]
2380 FOR I=1 TO NZ
2390 FOR J=1 TO NZ:BZ(I,J)=0:NEXT J
2400 BZ(I,I)=1
2410 NEXT I
2420 FOR I=1 TO NZ
2430 IZ=I
2440 IF AZ(I,I)=0 THEN 2450 ELSE 2510
2450 IZ=IZ+1:IF IZ>NZ THEN RZ=1:RETURN
2460 IF AZ(IZ,I)=0 THEN 2450
2470 FOR J=1 TO NZ
2480 SWAP AZ(I,J),AZ(IZ,J)
2490 SWAP BZ(I,J),BZ(IZ,J)
2500 NEXT J
2510 AII=AZ(I,I)
2520 FOR J=1 TO NZ
2530 AZ(I,J)=AZ(I,J)/AII
2540 BZ(I,J)=BZ(I,J)/AII
2550 NEXT J
2560 FOR K=1 TO NZ
2570 AKI=AZ(K,I):IF K=I THEN 2620
2580 FOR J=1 TO NZ
2590 AZ(K,J)=AZ(K,J)-AKI*AZ(I,J)
2600 BZ(K,J)=BZ(K,J)-AKI*BZ(I,J)
2610 NEXT J
2620 NEXT K
2630 NEXT I
2640 RZ=0
2650 RETURN
2660 '
2670 ' *** 楕円体 ***
2680 '
2690 *ELLIPSOID:
2700 IF M=1 THEN RETURN
2710 '
2720 FOR I=1 TO M
2730 FOR J=1 TO M:AZ(I,J)=COV(I,J):NEXT J
2740 NEXT I
2750 NZ=M:GOSUB *JACOBI
2760 '
2770 FOR I=1 TO M-1
2780 FOR J=I+1 TO M
2790 UO=VO(I):UL=VL(I)
2800 VO=VO(J):VL=VL(J)
2810 DU=VD(I):SU=VS(I)
2820 DV=VD(J):SV=VS(J)
2830 '
2840 GOSUB *DRAW.AXIS
2850 GOSUB *DRAW.ELLIPSE
2860 GOSUB *TEMP
2870 NEXT J
2880 NEXT I
2890 RETURN
2900 '
2910 ' ** 固有値 ( AZ==>BZ ) **
2920 '
2930 *JACOBI:' [ EIGEN-VECTOR: BZ(J,I) ]
2940 EPSL=.00001
2950 FOR I=1 TO NZ
2960 FOR J=1 TO NZ:BZ(I,J)=0:NEXT J
2970 BZ(I,I)=1
2980 NEXT I
2990 '
3000 CMAX=0
3010 FOR I=1 TO NZ
3020 FOR J=1 TO NZ
3030 IF CMAX<ABS(AZ(I,J)) THEN CMAX=ABS(AZ(I,J))
3040 NEXT J
3050 NEXT I
3060 EPS=CMAX*EPSL
3070 '
3080 LMAX=100
3090 LOOP=0
3100 SW=0
3110 WHILE LOOP<LMAX AND SW=0
3120 '
3130 FOR L=1 TO NZ-1
3140 FOR I=1 TO NZ-1
3150 J=I+L:IF J>NZ THEN 3340
3160 IF ABS(AZ(I,J))<EPS THEN 3330
3170 DIF=AZ(I,I)-AZ(J,J)
3180 IF DIF=0 THEN T=PI/4 ELSE T=1/2*ATN(2*AZ(I,J)/DIF)
3190 C=COS(T):S=SIN(T)
3200 FOR K=1 TO NZ
3210 A1=AZ(I,K):A2=AZ(J,K)
3220 AZ(I,K)= C*A1+S*A2
3230 AZ(J,K)=-S*A1+C*A2
3240 NEXT K
3250 FOR K=1 TO NZ
3260 A1=AZ(K,I):A2=AZ(K,J)
3270 AZ(K,I)= C*A1+S*A2
3280 AZ(K,J)=-S*A1+C*A2
3290 B1=BZ(K,I):B2=BZ(K,J)
3300 BZ(K,I)= C*B1+S*B2
3310 BZ(K,J)=-S*B1+C*B2
3320 NEXT K
3330 NEXT I
3340 NEXT L
3350 '
3360 SW=1
3370 FOR I=1 TO NZ-1
3380 FOR J=I+1 TO NZ
3390 IF ABS(AZ(I,J))>EPS THEN SW=0
3400 NEXT J
3410 NEXT I
3420 LOOP=LOOP+1
3430 '
3440 WEND
3450 RZ=0
3460 RETURN
3470 '
3480 ' *** 正射影 ***
3490 '
3500 *DRAW.ELLIPSE:
3510 'DRAW.COLOR=4
3520 WUO=UO-UL:WUL=UO+UL
3530 WVO=VO-VL:WVL=VO+VL
3540 WINDOW(WUO,-WVL)-(WUL,-WVO)
3550 VIEW(SX1,SY1)-(SX2,SY2)
3560 '
3570 'GOSUB *POLAR
3580 'GOSUB *EQUATOR
3590 'GOSUB *SECTION
3600 GOSUB *CONTOUR
3610 GOSUB *HYPERCUBE
3620 '
3630 WINDOW(0,0)-(639,399)
3640 VIEW(0,0)-(639,399)
3650 RETURN
3660 '
3670 ' *** 輪郭 ***
3680 '
3690 *CONTOUR:
3920 '
3930 DIF=COV(I,I)-COV(J,J)
3940 IF DIF=0 THEN TH=PI/4 ELSE TH=1/2*ATN(2*COV(I,J)/DIF)
3950 C=COS(TH):S=SIN(TH)
3960 '
3970 LAMBDA1=COV(I,I)*C*C+2*COV(I,J)*C*S+COV(J,J)*S*S
3980 LAMBDA2=COV(I,I)*S*S-2*COV(I,J)*C*S+COV(J,J)*C*C
3990 T=1:' [non-stochastic]
4000 AAA=SQR(T*LAMBDA1)
4010 BBB=SQR(T*LAMBDA2)
4020 '
4030 G=0
4040 FOR ANGLE=0 TO 2*PI+.01 STEP PI/180
4050 GX=AAA*COS(ANGLE)*C-BBB*SIN(ANGLE)*S+VO(I)
4060 GY=AAA*COS(ANGLE)*S+BBB*SIN(ANGLE)*C+VO(J)
4070 IF G=0 THEN PSET(GX,-GY),DRAW.COLOR:G=1
4080 LINE-(GX,-GY),DRAW.COLOR
4090 NEXT ANGLE
4100 RETURN
4640 '
4650 ' *** 超直方体 ***
4660 '
4670 *HYPERCUBE:
4680 T=1:' [non-stochastic]
4690 FOR IS=1 TO M:EDGE(IS)=SQR(T*AZ(IS,IS)):NEXT IS
4700 '
4710 FOR IS=0 TO 2^M-1
4720 FOR JS=1 TO M:S(JS)=-1:NEXT JS
4730 FOR JS=1 TO M
4740 IF (IS AND 2^(JS-1))=0 THEN S(JS)=1
4750 NEXT JS
4760 GOSUB *VERTEX:GXS=GX:GYS=GY
4770 '
4780 FOR JS=1 TO M:S0(JS)=S(JS):NEXT JS
4790 FOR JS=1 TO M
4800 FOR KS=1 TO M:S(KS)=S0(KS):NEXT KS
4810 S(JS)=-S(JS)
4820 GOSUB *VERTEX:GXE=GX:GYE=GY
4830 LINE(GXS,-GYS)-(GXE,-GYE),7
4850 NEXT JS
4860 NEXT IS
4870 RETURN
4880 '
4890 ' *** 頂点 ***
4900 '
4910 *VERTEX:
4920 GX=0:GY=0
4930 FOR LS=1 TO M
4940 GX=GX+BZ(I,LS)*EDGE(LS)*S(LS)
4950 GY=GY+BZ(J,LS)*EDGE(LS)*S(LS)
4960 NEXT LS
4970 GX=GX+VO(I):GY=GY+VO(J)
4980 RETURN
5350 '
5360 ' *** 座標軸 ***
5370 '
5380 *DRAW.AXIS:
5390 CLS 3
5400 SX1=59:SY1=360*(1-RY):SX2=580*RX+59:SY2=360
5410 LINE(SX1,SY1)-(SX2,SY2),GRP.COLOR,B
5420 RR=3:GOSUB *X.SCALE2:GOSUB *X.REF2
5430 RR=3:GOSUB *Y.SCALE2:GOSUB *Y.REF2
5440 RR=3:GOSUB *DOT.PLOT
5450 GOSUB *TITLE.BACK2
5460 RETURN
5470 '
5480 ' *** 等分目盛り (X) ***
5490 '
5500 *X.SCALE2:
5510 CU=(SX2-SX1)/DU/2
5520 IF KIND=0 THEN KARA=-RR:MADE=0
5530 IF KIND=1 THEN KARA=0 :MADE=RR
5540 IF KIND=2 THEN KARA=-RR:MADE=RR
5550 FOR K=0 TO DU*2
5560 LINE(CU*K+SX1,SY2+KARA)-(CU*K+SX1,SY2+MADE),GRP.COLOR
5570 LINE(CU*K+SX1,SY1-KARA)-(CU*K+SX1,SY1-MADE),GRP.COLOR
5580 NEXT K
5590 'GOSUB *X.REF2
5600 RETURN
5610 '
5620 ' *** 参照値の記入 (X) ***
5630 '
5640 *X.REF2:
5650 REF.COLOR=6
5660 UW=UL-UO
5670 FOR K=0 TO DU*2 STEP SU
5680 F=UW*(K/DU-1):F$=STR$(F)
5690 IF F>=0 THEN F$=MID$(F$,2)
5700 FL=LEN(F$)
5710 FOR L=1 TO FL
5720 GX=CU*K+59-FL*8/2+(L-1)*8:GY=23*16
5730 PUT(GX,GY),KANJI(ASC(MID$(F$,L,1))),PSET,REF.COLOR,0
5740 NEXT L
5750 NEXT K
5760 RETURN
5770 '
5780 ' *** 等分目盛り (Y) ***
5790 '
5800 *Y.SCALE2:
5810 CV=(SY2-SY1)/DV/2
5820 IF KIND=0 THEN KARA=0 :MADE=RR
5830 IF KIND=1 THEN KARA=-RR:MADE=0
5840 IF KIND=2 THEN KARA=-RR:MADE=RR
5850 FOR K=0 TO DV*2
5860 LINE(SX1+KARA,SY2-CV*K)-(SX1+MADE,SY2-CV*K),GRP.COLOR
5870 LINE(SX2-KARA,SY2-CV*K)-(SX2-MADE,SY2-CV*K),GRP.COLOR
5880 NEXT K
5890 'GOSUB *Y.REF2
5900 RETURN
5910 '
5920 ' *** 参照値の記入 (Y) ***
5930 '
5940 *Y.REF2:
5950 REF.COLOR=6
5960 VW=VL-VO
5970 FOR K=0 TO DV*2 STEP SV
5980 F=VW*(K/DV-1):F$=STR$(F)
5990 IF F>=0 THEN F$=MID$(F$,2)
6000 FL=LEN(F$)
6010 FOR L=1 TO FL
6020 GX=48-FL*8+(L-1)*8:GY=360-CV*K-8
6030 PUT(GX,GY),KANJI(ASC(MID$(F$,L,1))),PSET,REF.COLOR,0
6040 NEXT L
6050 NEXT K
6060 RETURN
6070 '
6080 ' *** プロット ***
6090 '
6100 *DOT.PLOT:
6110 WUO=UO-UL:WUL=UO+UL
6120 WVO=VO-VL:WVL=VO+VL
6130 WX=WUL-WUO
6140 BX=(WUL*SX1-WUO*SX2)/WX
6150 AX=(SX2-SX1)/WX
6160 WY=WVL-WVO
6170 BY=(WVL*SY2-WVO*SY1)/WY
6180 AY=(SY1-SY2)/WY
6190 '
6200 XX=AX*V(I)+BX
6210 YY=AY*V(J)+BY
6220 CIRCLE(XX,YY),RR,1
6230 PAINT(XX,YY),CLR,1
6240 CIRCLE(XX,YY),RR,CLR
6250 RETURN
6260 '
6270 ' *** タイトル ***
6280 '
6290 *TITLE.BACK2:
6300 LX=INT((580*RX+59)/8)
6310 LY=INT(360*(1-RY)/16)
6320 LZ=INT((290*RX+59)/8)
6330 L1$="ellipsoid projection of "
6340 L2$="v"+MID$(STR$(I),2)+"-"
6350 L3$="v"+MID$(STR$(J),2)+" plane"
6360 L$=L1$+L2$+L3$
6370 LOCATE LZ-LEN(L$)\2,LY-3:PRINT L$
6380 L$=UNIT$(J)
6390 IF LEN(L$)=0 THEN 6410
6400 LOCATE 7,LY-1:PRINT "("+L$+")"
6410 L$=UNIT$(I)
6420 IF LEN(L$)=0 THEN 6440
6430 LOCATE LX+3,21:PRINT "("+L$+")"
6440 '
6450 LOCATE LX+3,LY:PRINT "v components: "
6460 FOR K=1 TO M
6470 V$="v"+MID$(STR$(K),2)+"="
6480 LOCATE LX+3,LY+K+1:PRINT V$;:PRINT V(K)
6490 NEXT K
6500 RETURN
===================================